「《待ち行列モデルの標準形》」の版間の差分
Sakasegawa (トーク | 投稿記録) |
|||
| (4人の利用者による、間の6版が非表示) | |||
| 4行目: | 4行目: | ||
<center><table><tr><td align=center>[[画像:sk-0113-b-a-02-1.png]]</td></tr> | <center><table><tr><td align=center>[[画像:sk-0113-b-a-02-1.png]]</td></tr> | ||
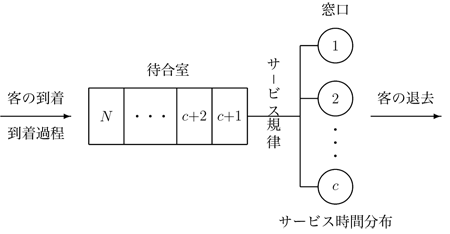
| − | <td align=center>図1:待ち行列の標準形 <math>*/*/{c}/{N}\, </math | + | <td align=center>図1:待ち行列の標準形 <math>*/*/{c}/{N}\, </math> |
| − | + | </td></table></center> | |
| + | <!-- | ||
| + | \begin{figure}[htb] \unitlength 1mm \thicklines \begin{center} \begin{picture}(130, 60)(0, 10) \put(0, 40){\vector(1, 0){20}} \put(105, 40){\vector(1, 0){20}} % \multiput(25, 32)(0, 16){2}{\line(1, 0){45}} \multiput(25, 32)(10, 0){2}{\line(0, 1){16}} \multiput(50, 32)(10, 0){3}{\line(0, 1){16}} \put(70, 40){\line(1, 0){15}} \put(85, 20){\line(0, 1){40}} \put(85, 20){\line(1, 0){5}} \put(85, 45){\line(1, 0){5}} \put(85, 60){\line(1, 0){5}} % \put(95, 20){\circle{10}} \put(95, 45){\circle{10}} \put(95, 60){\circle{10}} % \put(10, 45){\makebox(0, 0){客の到着}} \put(10, 35){\makebox(0, 0){到着過程}} \put(30, 40){\makebox(0, 0){$N$}} \multiput(38.75, 40)(3.75, 0){3}{\circle*{.7}} \put(55, 40){\makebox(0, 0){$c$+2}} \put(65, 40){\makebox(0, 0){$c$+1}} \put(47.5, 53){\makebox(0, 0){待合室}} \put(95, 70){\makebox(0, 0){窓口}} \put(95, 60){\makebox(0, 0){1}} \put(95, 45){\makebox(0, 0){2}} \multiput(95, 28.75)(0, 3.75){3}{\circle*{.7}} \put(95, 20){\makebox(0, 0){$c$}} \put(95, 10){\makebox(0, 0){サービス時間分布}} \put(115, 45){\makebox(0, 0){客の退去}} % \put(77.5, 48){\makebox(0, 0){\shortstack{サ\\\rule{.6pt}{7pt}\\ビ\\ス}}} \put(77.5, 35){\makebox(0, 0){\shortstack{規\\律}}} % \end{picture} \end{center} \caption{待ち行列の標準形 */*/{\it c}/{\it N}} \end{figure} | ||
| + | --> | ||
| − | '''到着過程とサービス時間分布''' 到着過程は通常, | + | |
| + | |||
| + | '''到着過程とサービス時間分布''' 到着過程は通常, 到着間隔の確率分布あるいは時間間隔 <math>(0, t]\, </math> の間に到着する客数の確率分布で表現される. よく用いられる到着間隔分布には, 時間間隔 <math>(0, t]\, </math> の間に到着する客数がポアソン分布に従う[[ポアソン到着]] (Poisson arrivals), 到着間隔が独立同一な一般分布に従う[[再生過程到着]] (renewal arrivals) や等間隔到着などがある. また, サービス時間分布に関しては, 独立同一な指数分布に従う[[指数サービス]] (exponential services), サービス時間が全て等しい一定時間サービス, 一般の分布に従うサービスなどがある. | ||
'''窓口の数と待合室の容量''' 窓口の数は通常, 有限であるが, 十分な数の窓口が用意されている[[無限窓口モデル]] (infinite-server model) もある. 待合室の容量に関しては通常, 無限である, すなわち十分に大きいと仮定されるが, 待合室の容量が有限である[[有限待合室モデル]] (finite-buffer model) もある. | '''窓口の数と待合室の容量''' 窓口の数は通常, 有限であるが, 十分な数の窓口が用意されている[[無限窓口モデル]] (infinite-server model) もある. 待合室の容量に関しては通常, 無限である, すなわち十分に大きいと仮定されるが, 待合室の容量が有限である[[有限待合室モデル]] (finite-buffer model) もある. | ||
| 16行目: | 21行目: | ||
<table width="70%"> | <table width="70%"> | ||
<tr> | <tr> | ||
| − | <td colspan="3" align="center"> | + | <td colspan="3" align="center">表1 ケンドールの記号<math>\mbox{A}/\mbox{B}/c/N/\mbox{X}\, </math></td> |
</tr> | </tr> | ||
<tr> | <tr> | ||
| 124行目: | 129行目: | ||
[2] D. G. Kendall, "Some Problems in the Theory of Queueus," ''Journal of the Royal Statistical Society, Series B'', '''13''' (1950), 151-185. | [2] D. G. Kendall, "Some Problems in the Theory of Queueus," ''Journal of the Royal Statistical Society, Series B'', '''13''' (1950), 151-185. | ||
| + | |||
| + | [3] 宮沢政清, 「待ち行列の数理とその応用」, 牧野書店, 2006. | ||
| + | |||
| + | [[category:待ち行列|まちぎょうれつもでるのひょうじゅんけい]] | ||
2007年9月21日 (金) 11:26時点における最新版
【まちぎょうれつもでるのひょうじゅんけい (standard models of queues) 】
標準的な待ち行列モデル 標準的な待ち行列モデル (queueing model) は, 客の到着を表す確率過程, すなわち到着過程 (arrival process) とそれぞれの客のサービス (service)に必要な時間(サービス時間という)の統計的性質, すなわちサービス時間分布 (service time distribution) という2つの確率的特性と, 待ち行列モデルの構造を表現するための, 窓口の数 (number of servers), サービスを待つ客のための待合室の容量 (capacity of waiting room), ならびに客にサービスを施す順序を表すサービス規律 (service discipline) を定めることによって得られる.
到着過程とサービス時間分布 到着過程は通常, 到着間隔の確率分布あるいは時間間隔 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle (0, t]\, }
の間に到着する客数の確率分布で表現される. よく用いられる到着間隔分布には, 時間間隔 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle (0, t]\, }
の間に到着する客数がポアソン分布に従うポアソン到着 (Poisson arrivals), 到着間隔が独立同一な一般分布に従う再生過程到着 (renewal arrivals) や等間隔到着などがある. また, サービス時間分布に関しては, 独立同一な指数分布に従う指数サービス (exponential services), サービス時間が全て等しい一定時間サービス, 一般の分布に従うサービスなどがある.
窓口の数と待合室の容量 窓口の数は通常, 有限であるが, 十分な数の窓口が用意されている無限窓口モデル (infinite-server model) もある. 待合室の容量に関しては通常, 無限である, すなわち十分に大きいと仮定されるが, 待合室の容量が有限である有限待合室モデル (finite-buffer model) もある.
| 表1 ケンドールの記号 | ||
|
|
||
| 記号 | 意味 | |
|
|
||
| 到着間隔分布ならびにサービス時間分布 | ポアソン到着あるいは指数サービス | |
| 等間隔到着あるいは一定時間サービス | ||
| 一般の分布に従う到着あるいはサービス | ||
| 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \mbox{GI}\, } | 再生過程到着あるいは独立同一な一般の分布に従うサービス | |
| 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \mbox{E}_k\, } | 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle k\, } 個の相をもつアーラン分布 | |
| 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \mbox{H}_k\, } | 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle k\, } 個の相をもつ超指数分布 | |
| 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \mbox{PH}\, } | 一般の相型分布 | |
| 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \mbox{MAP}\, } | マルコフ型到着過程 | |
| 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \mbox{M}^{[X]}\, } | ポアソン分布に従う集団到着 | |
|
|
||
| サービス規律構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \mbox{(X)}\, } | 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \mbox{FCFS}\, } | 先着順サービス |
| 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \mbox{FIFO}\, } | 先着順サービス (単一窓口の場合) | |
| 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \mbox{LCFS}\, } | 後着順サービス | |
| 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \mbox{LIFO}\, } | 後着順サービス (単一窓口の場合) | |
| 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \mbox{ROS}\, } | ランダム順サービス | |
| 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \mbox{PS}\, } | プロセッサシェアリング | |
|
|
||
サービス規律 サービス規律には, 到着順にサービスを行う最も標準的な規律である先着順サービス (first-come first-served service) 以外に, 到着とは逆の順序でサービスを行う後着順サービス (last-come first-served service), 到着順とは無関係に, でたらめな順序でサービスを行うランダム順サービス (random order service)やサービス施設の能力をシステム内の客で均等に分け合うプロセッサシェアリング (processor-sharing) などがある. また, 複数のタイプの客が到着し, タイプ間で優先権 (priority)がある場合も考えられている.
ケンドールの記号 待ち行列モデル (queueing model) はこれらの要素を組合わせることによって定めることができるが, この組み合わせを簡便に表現するための記法として, 通常, ケンドールの記号 (Kendall's notation) が用いられる. ケンドールの記号は A/B/構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle c/N\, } という形をもっており, Aは到着間隔分布, Bはサービス時間分布, 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle c\, } は窓口の数, 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle N\, } は窓口と待合室の容量の和を表す. さらに, これらに加えて, サービス規律を付加することもある. これらを表す記号を表1に示す.
例えば M/M/3/10/FCFS (あるいは FCFS M/M/3/10) は, ポアソン到着, 指数サービス, 窓口が3つで待合室の容量が7であり, サービスが先着順で行われる待ち行列モデルを表し, GI/G/1/構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \infty\, } /LCFS (あるいは LCFS GI/G/1/構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \infty\, } ) は, 再生過程到着, 一般分布サービス, 窓口が1つで待合室の容量に制限がなく, サービスが後着順で行われる待ち行列モデルを表す. 特に, 待合室の容量に制限がない場合 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \infty\, } を省略し, またサービス規律がFCFS の場合, これを省略することが多い. 例えば M/D/2 はポアソン到着, 一定サービス, 窓口が2つで待合室の容量に制限がなく, サービスが先着順で行われる待ち行列モデルを表す.
参考文献
[1] D. Gross and C. M. Harris, Fundamentals of Queueing Theory, Third Edition, John Wiley & Sons, 1998.
[2] D. G. Kendall, "Some Problems in the Theory of Queueus," Journal of the Royal Statistical Society, Series B, 13 (1950), 151-185.
[3] 宮沢政清, 「待ち行列の数理とその応用」, 牧野書店, 2006.