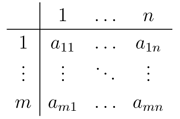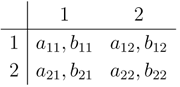「《ゲームの解の計算》」の版間の差分
| (4人の利用者による、間の9版が非表示) | |||
| 6行目: | 6行目: | ||
| − | :< | + | <center> |
| + | |||
| + | [[画像:sk-0079-a-g-11-1.png]] | ||
| + | |||
| + | </center> | ||
| + | |||
| + | <!-- | ||
| + | \[ | ||
| + | \begin{array}{c|ccc} | ||
& 1 & \ldots & n \\ \hline | & 1 & \ldots & n \\ \hline | ||
1 & a_{11} & \ldots & a_{1n} \\ | 1 & a_{11} & \ldots & a_{1n} \\ | ||
\vdots & \vdots & \ddots & \vdots \\ | \vdots & \vdots & \ddots & \vdots \\ | ||
m & a_{m1} & \ldots & a_{mn} | m & a_{m1} & \ldots & a_{mn} | ||
| − | \end{array}\ | + | \end{array} |
| + | \] | ||
| + | --> | ||
| + | |||
| 17行目: | 28行目: | ||
| − | + | <center> | |
| + | <math>\begin{array}{ll} | ||
\mbox{maximize} & v \\ | \mbox{maximize} & v \\ | ||
\mbox{subject to} & a_{1j}p_1 + a_{2j}p_2 + \ldots + a_{mj}p_m \geq v \ (j = 1, 2, \ldots, n), \\ | \mbox{subject to} & a_{1j}p_1 + a_{2j}p_2 + \ldots + a_{mj}p_m \geq v \ (j = 1, 2, \ldots, n), \\ | ||
& p_1 + p_2 + \ldots + p_m = 1,\;\; p_1, p_2, \ldots, p_m \geq 0. | & p_1 + p_2 + \ldots + p_m = 1,\;\; p_1, p_2, \ldots, p_m \geq 0. | ||
| − | \end{array}\, </math> | + | \end{array}\, </math> |
| + | </center> | ||
| 27行目: | 40行目: | ||
| − | + | <center> | |
| + | <math>\max_{0 \leq p_1 \leq 1} \min | ||
\{a_{11}p_1 + a_{21}(1-p_1), a_{12}p_1 + a_{22}(1-p_1), | \{a_{11}p_1 + a_{21}(1-p_1), a_{12}p_1 + a_{22}(1-p_1), | ||
\ldots , a_{1n}p_1 + a_{2n}(1-p_1) \}\, </math> | \ldots , a_{1n}p_1 + a_{2n}(1-p_1) \}\, </math> | ||
| + | </center> | ||
| 39行目: | 54行目: | ||
| − | :< | + | <center> |
| + | [[画像:sk-0079-a-g-11-2.png]] | ||
| + | |||
| + | </center> | ||
| + | |||
| + | <!-- | ||
| + | \[ \begin{array}{c|cc} | ||
& 1 & 2 \\ \hline | & 1 & 2 \\ \hline | ||
1 & a_{11}, b_{11} & a_{12}, b_{12} \\ | 1 & a_{11}, b_{11} & a_{12}, b_{12} \\ | ||
2 & a_{21}, b_{21} & a_{22}, b_{22} \\ | 2 & a_{21}, b_{21} & a_{22}, b_{22} \\ | ||
| − | \end{array}\ | + | \end{array} \] |
| + | --> | ||
| 51行目: | 73行目: | ||
| − | 図1:2人ゲームのマックスミニ戦略およびナッシュ均衡の計算 | + | <center><table><tr><td align=center>[[画像:0079-a-g-11fig.png|center|図1:2人ゲームのマックスミニ戦略およびナッシュ均衡の計算]]</td></tr> |
| − | + | <td align=center>図1:2人ゲームのマックスミニ戦略およびナッシュ均衡の計算 | |
| + | </td></table></center> | ||
[[ナッシュ均衡]]は両者の最適反応の交点 (図1(b)の3つの交点) で与えられるから, この場合には, 純戦略に対応する <math>p=q=1\, </math> と <math>p=q=0\, </math> および, <math>A_1 = A_2\, </math> かつ <math>B_1 = B_2\, </math> を満たす混合戦略に対応する <math>p=(b_{22}-b_{21})/(b_{11}-b_{12} + b_{22}-b_{21})\, </math> , <math>q=(a_{12}-a_{22})/(a_{21}-a_{11} + a_{12}-a_{22})\, </math> の合計3通りのナッシュ均衡が存在する. <math>a_{11}>a_{21}, a_{12}<a_{22}, b_{11}>b_{12}, b_{21}<b_{22}\, </math>以外の場合など, 詳しくは, 例えば [4] を参照. | [[ナッシュ均衡]]は両者の最適反応の交点 (図1(b)の3つの交点) で与えられるから, この場合には, 純戦略に対応する <math>p=q=1\, </math> と <math>p=q=0\, </math> および, <math>A_1 = A_2\, </math> かつ <math>B_1 = B_2\, </math> を満たす混合戦略に対応する <math>p=(b_{22}-b_{21})/(b_{11}-b_{12} + b_{22}-b_{21})\, </math> , <math>q=(a_{12}-a_{22})/(a_{21}-a_{11} + a_{12}-a_{22})\, </math> の合計3通りのナッシュ均衡が存在する. <math>a_{11}>a_{21}, a_{12}<a_{22}, b_{11}>b_{12}, b_{21}<b_{22}\, </math>以外の場合など, 詳しくは, 例えば [4] を参照. | ||
| − | <math>2 \times 2\, </math> よりも大きな利得行列をもつ2人非ゼロ和ゲームのナッシュ均衡を求める方法としては, [[ | + | <math>2 \times 2\, </math> よりも大きな利得行列をもつ2人非ゼロ和ゲームのナッシュ均衡を求める方法としては, [[シャープレイのラベル法|シャープレイ(L. S. Shapley)のラベル法]](Shapley's labelling method) [6] がある. <math>3\, </math>人以上のプレイヤーからなる[[戦略形ゲーム]]においては, [[不動点アルゴリズム]]を用いて, ナッシュ均衡の近似値を計算することができる. [7] を参照. |
[[展開形ゲーム]]における[[部分ゲーム完全均衡]], [[完全均衡]], [[逐次均衡]]などの計算については, [4] を参照. | [[展開形ゲーム]]における[[部分ゲーム完全均衡]], [[完全均衡]], [[逐次均衡]]などの計算については, [4] を参照. | ||
| 66行目: | 89行目: | ||
| − | + | <center> | |
| + | <math>\begin{array}{lll} | ||
\mbox{minimize} & e \\ | \mbox{minimize} & e \\ | ||
\mbox{subject to} & x(S) + e \geq v(S) & | \mbox{subject to} & x(S) + e \geq v(S) & | ||
| 72行目: | 96行目: | ||
& x(N) = v(N). | & x(N) = v(N). | ||
\end{array}\, </math> | \end{array}\, </math> | ||
| + | </center> | ||
問題<math>P_1\, </math>の最適解において, <math>e \leq 0\, </math> となっているならば, ゲーム<math>(N, v)\, </math>のコアは空集合ではなく, <math>e \leq 0\, </math> を満たす実行可能解すべてからなる集合がコアとなる. また, コアが空であろうと非空であろうと, 問題<math>P_1\, </math>の最適解の全体はゲーム<math>(N, v)\, \, </math>の[[最小コア (ゲーム理論の)|最小コア]]になる. | 問題<math>P_1\, </math>の最適解において, <math>e \leq 0\, </math> となっているならば, ゲーム<math>(N, v)\, </math>のコアは空集合ではなく, <math>e \leq 0\, </math> を満たす実行可能解すべてからなる集合がコアとなる. また, コアが空であろうと非空であろうと, 問題<math>P_1\, </math>の最適解の全体はゲーム<math>(N, v)\, \, </math>の[[最小コア (ゲーム理論の)|最小コア]]になる. | ||
| − | [[仁]]は, 線形計画問題を繰り返し解く[[ | + | [[仁]]は, 線形計画問題を繰り返し解く[[コペロウィッツのアルゴリズム]] (Kopelowitz' algorithm) [2] によって求められる. まず, 問題<math>P_1\, </math>の最適解における<math>e\, </math>の値を<math>e_1\, </math>とする. もしも最適解が唯一でない場合は, すべての最適解を求め, 不等式制約条件がその全最適解において等号で成立しているような<math>S\, </math>の族を<math>A_1\, </math>とおく. さらに, <math>A_1\, </math>に含まれるすべての<math>S\, </math>に対して問題<math>P_1\, </math>の制約式 <math>x(S) + e \geq v(S)\, </math> を <math>x(S) + e_1 = v(S)\, </math> に置き換えて新たな問題<math>P_2\, </math>をつくり, その最適解を求める. このプロセスを繰り返し, あるステップで, 最適解が唯一であればそれが仁の配分である. このアルゴリズムは<math>n-1\, </math>回以内の繰り返しで必ず終了する. ただし, 1回の繰り返しの中での計算量は膨大になることがある. 仁のより効率的な計算方法については, [1], [5] を参照. |
[[シャープレイ値]]の計算方法については, [3] を参照. | [[シャープレイ値]]の計算方法については, [3] を参照. | ||
| 98行目: | 123行目: | ||
[7] Z. -F. Yang, ''Computing Equilibria and Fixed Points'', Kluwer Academic Publishers, 1999. | [7] Z. -F. Yang, ''Computing Equilibria and Fixed Points'', Kluwer Academic Publishers, 1999. | ||
| + | |||
| + | [[category:ゲーム理論|げーむのかいのけいさん]] | ||
2007年8月9日 (木) 14:48時点における最新版
【ゲームのかいのけいさん (computation of solutions of games) 】
1. 2人ゼロ和ゲームのマックスミニ戦略の計算
プレイヤー1の混合戦略を構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle p = (p_1, p_2, \ldots, p_m)\, }
, プレイヤー2の混合戦略を構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle q = (q_1, q_2, \ldots, q_n)\, }
, 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle 0 \leq p_i, q_j \leq 1 \, }
, 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \textstyle \sum_{i=1}^{m} p_i = 1\, }
, 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \textstyle \sum_{j=1}^{n} q_j = 1\, }
とするとき, プレイヤー1のマックスミニ戦略は, 次の線形計画問題の最適解として得られ, 最適値がマックスミニ値となる.
構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \begin{array}{ll} \mbox{maximize} & v \\ \mbox{subject to} & a_{1j}p_1 + a_{2j}p_2 + \ldots + a_{mj}p_m \geq v \ (j = 1, 2, \ldots, n), \\ & p_1 + p_2 + \ldots + p_m = 1,\;\; p_1, p_2, \ldots, p_m \geq 0. \end{array}\, }
プレイヤー2のミニマックス戦略はこの問題の双対問題を解いて求められる. 少なくとも一方のプレイヤーの純戦略が2個だけである場合には, マックスミニ戦略, ミニマックス戦略はより簡単に計算することができる. 例えば, 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle m=2\, }
とすると, プレイヤー1のマックスミニ戦略は,
構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \max_{0 \leq p_1 \leq 1} \min \{a_{11}p_1 + a_{21}(1-p_1), a_{12}p_1 + a_{22}(1-p_1), \ldots , a_{1n}p_1 + a_{2n}(1-p_1) \}\, }
の解となる. いま, 各jについて 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle a_{1j}p_1 + a_{2j}(1-p_1)\, }
のグラフを描き, 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle n\, }
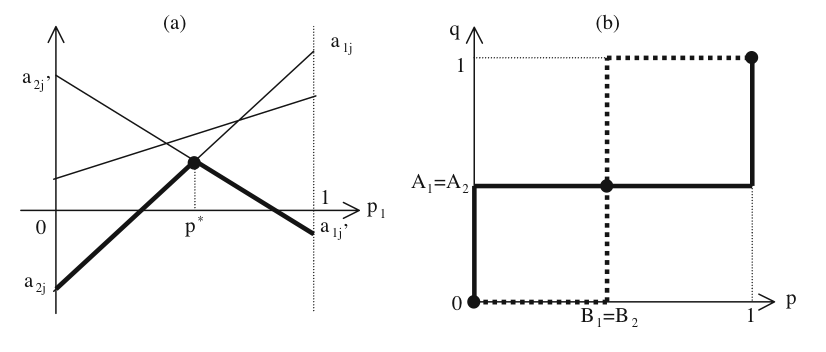
個のグラフの最小の部分をたどるグラフ (図1(a)の太線) を描く. このグラフの最大値を与える構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle p_1\, }
を構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle p^*\, }
とすると, プレイヤー1のマックスミニ戦略は構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle (p^*, 1-p^*)\, }
で与えられる. 図1(a)はの場合である. プレイヤー2については, 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle p^*\, }
を与える2つの戦略について同様の計算を行ってミニマックス戦略を求めることができる. 詳しくは, 例えば [4] を参照.
2. 非ゼロ和ゲームのナッシュ均衡の計算
次のような 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle 2 \times 2\, } の利得双行列をもつ2人非ゼロ和ゲームを考える.
プレイヤー1, 2の混合戦略を各々 , 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle (q, 1-q)\, } , 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle 0 \leq p, q \leq 1\, } とする.
とおくと, プレイヤー1の利得の期待値 (期待利得) は 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle p A_1 + (1-p) A_2\, } となるから, 最適反応は のとき , 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle A_1 = A_2\, } のとき , のとき 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle p=0\, } となる. 同様にプレイヤー2の最適反応は, とおいて, のとき , のとき のとき 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle q=0\, } となる. 従って, 両者の最適反応は, もし, であれば, 図1(b) のように表現される.
| 図1:2人ゲームのマックスミニ戦略およびナッシュ均衡の計算 |
ナッシュ均衡は両者の最適反応の交点 (図1(b)の3つの交点) で与えられるから, この場合には, 純戦略に対応する 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle p=q=1\, }
と および, かつ を満たす混合戦略に対応する 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle p=(b_{22}-b_{21})/(b_{11}-b_{12} + b_{22}-b_{21})\, }
, の合計3通りのナッシュ均衡が存在する. 以外の場合など, 詳しくは, 例えば [4] を参照.
よりも大きな利得行列をもつ2人非ゼロ和ゲームのナッシュ均衡を求める方法としては, シャープレイ(L. S. Shapley)のラベル法(Shapley's labelling method) [6] がある. 人以上のプレイヤーからなる戦略形ゲームにおいては, 不動点アルゴリズムを用いて, ナッシュ均衡の近似値を計算することができる. [7] を参照.
展開形ゲームにおける部分ゲーム完全均衡, 完全均衡, 逐次均衡などの計算については, [4] を参照.
3. 提携形 (特性関数形) ゲームの解の計算
提携形ゲームのコアの配分 を計算するために, まず 本の制約式をもつ次の線形計画問題構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle P_1\, } を考える (構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \textstyle |N|=n, x(S)=\sum_{i \in S} x_i \, } ).
構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \begin{array}{lll} \mbox{minimize} & e \\ \mbox{subject to} & x(S) + e \geq v(S) & (S \subset N, \ S \neq N, \emptyset), \\ & x(N) = v(N). \end{array}\, }
問題構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle P_1\, }
の最適解において, 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle e \leq 0\, }
となっているならば, ゲーム構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle (N, v)\, }
のコアは空集合ではなく, 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle e \leq 0\, }
を満たす実行可能解すべてからなる集合がコアとなる. また, コアが空であろうと非空であろうと, 問題構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle P_1\, }
の最適解の全体はゲーム構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle (N, v)\, \, }
の最小コアになる.
仁は, 線形計画問題を繰り返し解くコペロウィッツのアルゴリズム (Kopelowitz' algorithm) [2] によって求められる. まず, 問題構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle P_1\, } の最適解における構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle e\, } の値を構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle e_1\, } とする. もしも最適解が唯一でない場合は, すべての最適解を求め, 不等式制約条件がその全最適解において等号で成立しているような構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle S\, } の族を構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle A_1\, } とおく. さらに, 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle A_1\, } に含まれるすべての構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle S\, } に対して問題構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle P_1\, } の制約式 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle x(S) + e \geq v(S)\, } を 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle x(S) + e_1 = v(S)\, } に置き換えて新たな問題構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle P_2\, } をつくり, その最適解を求める. このプロセスを繰り返し, あるステップで, 最適解が唯一であればそれが仁の配分である. このアルゴリズムは構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle n-1\, } 回以内の繰り返しで必ず終了する. ただし, 1回の繰り返しの中での計算量は膨大になることがある. 仁のより効率的な計算方法については, [1], [5] を参照.
シャープレイ値の計算方法については, [3] を参照.
参考文献
[1] G. Bruyneel, "Computation of the Nucleolus of a Game by Means of Minimal Balanced Sets," Operations Research Verfahren, 34 (1979), 35-51.
[2] A. Kopelowitz, "Computation of the Kernels of Simple Games and the Nucleolus of n-Person Games," "Research Program in Game Theory and Mathematical Economics", RM 31, The Hebrew University of Jerusalem, 1967.
[3] 武藤滋夫, 小野理恵, 「投票システムのゲーム分析」, 日科技連出版社, 1998.
[4] 岡田章, 「ゲーム理論」, 有斐閣, 1996.
[5] J. K. Sankaran, "On Finding the Nucleolus of an n-Person Cooperative Game," International Journal of Game Theory, 19 (1991), 329-338.
[6] L. S. Shapley, "A Note on the Lemke-Howson Algorithm," Mathematical Programming Study, 1 (1974), 175-189.
[7] Z. -F. Yang, Computing Equilibria and Fixed Points, Kluwer Academic Publishers, 1999.