「待ち行列ネットワーク」の版間の差分

提供: ORWiki
ナビゲーションに移動 検索に移動
 
(4人の利用者による、間の6版が非表示)
1行目: 1行目:
 
'''【まちぎょうれつねっとわーく (queueing network)】'''
 
'''【まちぎょうれつねっとわーく (queueing network)】'''
 +
=== 概要 ===
  
−
複数の待ち行列システムが, 直列, リング状あるいはネットワーク状に組み合わされた数学モデル. 情報ネットワーク, コンピュータシステム, FMS (flexible manufacturing system) を始めとする生産システム, 交通システムなどの複合システムにおける「待ち」現象の確率的振る舞いを取り扱う. 待ち時間, 待ち行列長, スループットなどの性能評価量を算出するのに用いられる.
+
複数の待ち行列システムが，直列，リング状あるいはネットワーク状に組み合わされた数学モデル．情報ネットワーク，コンピュータシステム，FMS（flexible manufacturing system）を始めとする生産システム，交通システムなどの複合システムにおける「待ち」現象の確率的振る舞いを取り扱う．[[待ち時間]]，[[待ち行列長]]，スループットなどの性能評価量を算出するのに用いられる．
  
−
\中項目{待ち行列ネットワーク}{待ち行列ネットワーク}{まちぎょうれつねっ
+
=== 詳説 ===
−
とわーく}{queueing network}
+
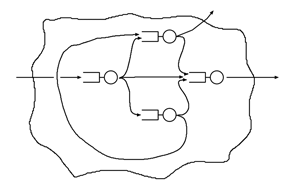
　複数の待ち行列システム(以下ノードと表記)が, 図1のようにネットワーク上に結合された数学モデルを[[待ち行列ネットワーク]] (queueing network あるいは network of queues) と呼ぶ.
  
−
複数の待ち行列システム(以下ノードと表記)が，図
 
−
\ref{B-B-01+queueing-network}のようにネットワーク上に結合された数学モ
 
−
デルを[[待ち行列ネットワーク]]
 
−
(queueing networkあるいはnetwork of queues)と呼ぶ．
 
−
%
 
−
\begin{figure}[htbp]
 
−
\begin{center}
 
−
\includegraphics[bbllx=0, bblly=185mm, bburx=180mm,
 
−
bbury=280mm, height=50mm]{network.eps}
 
−
\caption{待ち行列ネットワーク}
 
−
\label{B-B-01+queueing-network}
 
−
\end{center}
 
−
\end{figure}
 
  
−
各ノード間の移動は通常確率的に選択される．例えばノード$i$から $j$は確
+
<center><table><tr><td align=center>[[画像:0123-Network.png|center|図１：待ち行列ネットワーク]]</td></tr>
−
率$r_{ij}$で移動する．この確率を\yougolink{B-B-02}{経路選択確率}{経路選択確率}(routing)あるいは分岐確率(branching
+
<td align=center>図１：待ち行列ネットワーク</td></table></center>
−
probability)と呼ぶ．特にネットワーク外を表現するのにノード0と記す．
 
−
このモデルの確率的な振る舞いを解析し，待ち時間・待ち行列長などに関する
 
−
性能評価量の算出が可能になる．待ち行列ネットワークの中で，特に図
 
−
\ref{B-B-01+tandem-model}のように直列に繋がったモデルを
 
−
\yougolink{B-B-01}{直列型待ち行列}{直列型待ち行列} (tandem queueあるい
 
−
はseries queue)と呼ぶ．
 
  
−
\begin{figure}[htbp]
 
−
\begin{center}
 
−
\includegraphics[bbllx=0, bblly=210mm, bburx=230mm, bbury=260mm,
 
−
height=40mm]{tandem.eps}
 
−
\caption{直列型待ち行列}
 
−
\label{B-B-01+tandem-model}
 
−
\end{center}
 
−
\end{figure}
 
  
−
これらのモデルにおいては，あるノードからの退去過程は他のノードへの到着
+
　各ノード間の移動は通常確率的に選択される. 例えばノード <math>i</math> から <math>j</math> は確率 <math>r_{ij}</math> で移動する. [[経路選択確率]] (routing probability) あるいは分岐確率 (branching probability) と呼ぶ. 特にネットワーク外を表現するのにノード0と記す．このモデルの確率的な振る舞いを解析し, 待ち時間・待ち行列長・スループットなどに関する性能評価量を算出が可能となる. 特に図2のように直列につながったモデルを[[直列型待ち行列]](queueing networkあるいはnetwork of queues)と呼ぶ．
−
過程になることからノード間の従属性が生じる．さらにはネットワークにフィー
 
−
ドバック・ループがある場合には，退去した客が再度到着する可能性もあり，
 
−
到着客間にも従属性が生じる．これらのことから個別のノードを取り出し，解
 
−
析するのは不可能であり，ネットワーク全体を捉えた解析が必要である．これ
 
−
までに解析的にはマルコフ性を保持しながら，\yougolink{B-B-02}{積形式解}
 
−
{積形式解}が得られる範囲内で，現実のシステムにより近いモデルが次々と発
 
−
表されて来た．
 
  
−
待ち行列ネットワークは，外部との関わり方で\yougolink{B-B-01}{開放型ネッ
+
<center><table><tr><td align=center>[[画像:sk-0123-b-b-01-1.png]]</td></tr>
−
トワーク}{開放型ネットワーク}(open network)と\yougolink{B-B-01}{閉鎖型
+
<td align=center>図２：直列型待ち行列<br></td></table></center>
−
ネットワーク} {閉鎖型ネットワーク}(closed network)に分類が可能である．
 
−
開放型ネットワークにおいてはネットワーク外からの客の到着があり，またネッ
 
−
トワーク外への退去もある．従ってネットワーク内の総客数は可変であり，一
 
−
定ではない．これは例えば蓄積交換型のパケット交換網においては，パケット
 
−
送信要求の発生が客のネットワークへの流入に相当し，各交換機およびそれに
 
−
付随するバッファが各ノードに対応する．従って目的局に受信されることが，
 
−
ネットワークからの退去に当たる．一方閉鎖型ネットワークにおいてはネット
 
−
ワーク外からの客の到着，外への退去はない．従って総客数が常に一定に保た
 
−
れる．これは例えば一定台数の機械から構成されるシステムにおいて機械の故
 
−
障・修理を考慮した性能評価を行なう際に用いられる．あるいはマルチプログ
 
−
ラミング環境下で動作する計算機システムのように，内部にCPU，I/O機器など
 
−
のサーバおよびそれに付随した待ち行列があり，総客数は一定に保たれている
 
−
場合に相当する．計算が完了したジョブ／トランザクションはネットワークか
 
−
ら消滅するが，それと同時にネットワーク外のバッファに貯えられていたジョ
 
−
ブ・トランザクションが投入され，結果として総数が変わらないような場合に
 
−
も適用が可能であり，計算機アーキテクチュアなどの評価に用いられた．閉鎖
 
−
型ネットワークで，機械修理問題に見られるように，稼動状態，修理待ち状態，
 
−
検査待ち状態のそれぞれに対応するノードを順番に訪問し，客の流れが同一方
 
−
向で，訪問する待ち行列の順番が一定な直列型待ち行列を特に循環型待ち行列
 
−
(図\ref{B-B-01+cyclic-queue}参照)と呼ぶ．
 
  
−
\begin{figure}[htbp]
+
<!--
−
\begin{center}
+
\begin{figure}[htbp] \begin{center} %\includegraphics[bbllx=0, bblly=210mm, bburx=230mm, bbury=260mm, %height=40mm]{. . /b-b/tandem.eps} \setlength{\unitlength}{1mm} \begin{picture}(108, 20)(0, -10) \thicklines \put(0, 0){\vector(1, 0){8}} \multiput(9, -2.5)(0, 5){2}{\line(1, 0){7}} \put(16, -2.5){\line(0, 1){5}} \put(16, 0){\line(1, 0){2}} \put(21, 0){\circle{6}} \put(24, 0){\vector(1, 0){8}} \multiput(33, -2.5)(0, 5){2}{\line(1, 0){7}} \put(40, -2.5){\line(0, 1){5}} \put(40, 0){\vector(2, 3){4}} \put(40, 0){\vector(2, -3){4}} \put(47, 7.5){\circle{6}} \put(47, -7.5){\circle{6}} \put(47, 0){\makebox(0, 1.2){$\vdots$}} \put(50, 6){\vector(2, -3){4}} \put(50, -6){\vector(2, 3){4}} \multiput(55, -2.5)(0, 5){2}{\line(1, 0){7}} \put(62, -2.5){\line(0, 1){5}} \put(62, 0){\line(1, 0){2}} \put(67, 0){\circle{6}} \put(70, 0){\vector(1, 0){5}} \put(80, 0){\makebox(0, 0){$\cdots$}} \multiput(84, -2.5)(0, 5){2}{\line(1, 0){7}} \put(91, -2.5){\line(0, 1){5}} \put(91, 0){\line(1, 0){2}} \put(96, 0){\circle{6}} \put(99, 0){\vector(1, 0){9}} \end{picture} \end{center} \caption{直列型待ち行列} \label{B-B-01+tandem-model} \end{figure}  
−
\includegraphics[bbllx=0, bblly=190mm, bburx=130mm, bbury=270mm,  
+
-->
−
height=60mm]{cyclic.eps}
 
−
\caption{循環型待ち行列}
 
−
\label{B-B-01+cyclic-queue}
 
−
\end{center}
 
−
\end{figure}
 
−
%
 
  
−
また図\ref{B-B-01+central-server-model}に示すように，閉鎖型ネットワー
+
　これらのモデルにおいては，あるノードからの退去過程は他のノードへの到着過程になることからノード間の従属性が生じる．さらにはネットワークにフィー
−
クで特に計算機システムをモデル化するために，中央に位置するサーバ(CPU
+
ドバック・ループがある場合には，退去した客が再度到着する可能性もあり，到着客間にも従属性が生じる．これらのことから個別のノードを取り出し，解
−
に相当)と複数の他のサーバおよびそれに付随する待ち行列(入出力機器など
+
析するのは不可能であり，ネットワーク全体を捉えた解析が必要である．これまでに解析的にはマルコフ性を保持しながら，[[積形式解]]が得られる範囲内で，現実のシステムにより近いモデルが次々と発表されて来た．
−
の周辺機器に相当)からなり，客がこれらの間を交互に行き来するモデルを
+
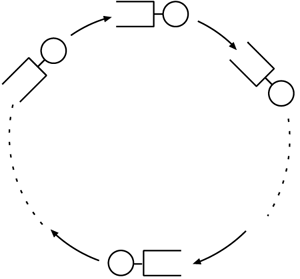
　待ち行列ネットワークは，外部との関わり方で[[開放型ネットワーク]](open network)と[[閉鎖型ネットワーク]](closed network)に分類が可能である．開放型ネットワークにおいてはネットワーク外からの客の到着があり，またネットワーク外への退去もある．従ってネットワーク内の総客数は可変であり，一定ではない．これは例えば蓄積交換型のパケット交換網においては，パケット送信要求の発生が客のネットワークへの流入に相当し，各交換機およびそれに付随するバッファが各ノードに対応する．従って目的局に受信されることが，ネットワークからの退去に当たる．一方閉鎖型ネットワークにおいてはネットワーク外からの客の到着，外への退去はない．従って総客数が常に一定に保たれる．これは例えば一定台数の機械から構成されるシステムにおいて機械の故障・修理を考慮した性能評価を行なう際に用いられる．あるいはマルチプログラミング環境下で動作する計算機システムのように，内部にCPU，I/O機器などのサーバおよびそれに付随した待ち行列があり，総客数は一定に保たれている場合に相当する．計算が完了したジョブ／トランザクションはネットワークから消滅するが，それと同時にネットワーク外のバッファに貯えられていたジョブ・トランザクションが投入され，結果として総数が変わらないような場合にも適用が可能であり，計算機アーキテクチュアなどの評価に用いられた．閉鎖型ネットワークで，機械修理問題に見られるように，稼動状態，修理待ち状態，検査待ち状態のそれぞれに対応するノードを順番に訪問し，客の流れが同一方向で，訪問する待ち行列の順番が一定な直列型待ち行列を特に循環型待ち行列(図3参照)と呼ぶ．
−
\yougolink{B-B-01}{セントラルサーバモデル}{セントラルサーバモデル}と呼
 
−
ぶ．
 
  
−
\begin{figure}[htbp]
 
−
\begin{center}
 
−
\includegraphics[bbllx=0, bblly=210mm, bburx=230mm, bbury=260mm,
 
−
height=40mm]{central.eps}
 
−
\caption{セントラルサーバモデル}
 
−
\label{B-B-01+central-server-model}
 
−
\end{center}
 
−
\end{figure}
 
  
−
また単一待ち行列モデルで客の母集団が有限である場合も，閉鎖型ネットワー
 
−
クの一例と見ることも可能である．
 
  
−
さらに客が優先権，待ち行列ネットワーク内の移動経路などの属性により複数
 
−
クラスに分類され，一部のクラスに属する客に関しては開放型で，他のクラス
 
−
の客に関しては閉鎖型のネットワークを\yougolink{B-B-01}{混合型ネットワー
 
−
ク}{混合型ネットワーク}と呼ぶ．
 
  
−
待ち行列ネットワークの別の分類として，各ノードで許容される待ち行列長に
+
<center><table><tr><td align=center>[[画像:0123-Cyclic.png|center|図３：循環型待ち行列]]</td></tr>
−
関する制限の有無に依るものがある．制限が無い場合には適当なモデル化の仮
+
<td align=center><br>図３：循環型待ち行列</td></table></center>
−
定を設ければ積形式解を用いた実用的な計算
 
−
が可能であるが，制限がある場合には，ブロッキングが発生し，ノード間のよ
 
−
り一層複雑な従属性が生じ，有効な解析法は存在しない．このような場合には
 
−
近似的なアプローチを取らざるを得ない．ブロッキングとは，次に訪問するノー
 
−
ドの待合室が一杯のときに移動が妨げられることを言う．この結果，モデルに
 
−
よっては元のサーバが次の客へのサービスを行なえない．客がいるにも拘わら
 
−
ずサービスが開始されない．これは例えば多段工程からなる生産ラインにおけ
 
−
る，各工程における仕掛品置き場のように大容量のバッファがないシステムに
 
−
相当する．一方通信網においては，ブロッキングが発生すると客であるパケッ
 
−
ト・メッセージなどは消滅する．
 
  
−
待ち行列ネットワークは，従来単一待ち行列システムでモデル化されていた生
 
−
産・通信・コンピュータ・輸送・交通システムのネットワーク化に伴い，その
 
−
重要性が増しており，特に積形式解を持つモデルの数値計算を支援するソフト
 
−
ウェア・パッケージなども提供されている．
 
  
−
%\begin{thebibliography}{99}
+
　また図4に示すように, 計算機システムをモデル化した閉鎖型ネットワークで, 中央に位置するサーバ (CPU に相当) と複数の他のサーバおよびそれに付随する待ち行列 (入出力機器などの周辺機器に相当) からなり, 客がこれらの間を交互に行き来するモデルを[[セントラルサーバモデル]]と呼ぶ.  
−
%\bibitem{M12+MATSUI2}
 
−
%  A. V. Aho, J. E. Hopcraft and J. D. Ullman,      % and の前に「,」は入れない
 
−
%  {\it The Design and Analysis of Computer Algorithms},
 
−
%  Addison-Wesley, 1974.                            % 本の題は斜体
 
−
%-------------------------- 英語単行本の章 ------------------------------
 
−
%\bibitem{M12+MATSUI3}
 
−
%  R. K. Ahuja, T. L. Magnanti and J. B. Orlin,    %
 
−
%  ``Network Flows,''                              % 章名は 「``題目,''」
 
−
%  in {\it Optimization},                          % 「in」を入れる
 
−
%  G. L. Nemhauser, A. H. G. Rinooy Kan and M. J. Todd, eds.,
 
−
%  North-Holland, 1989.                            % 編者は「 eds.,」とする
 
−
%-------------------------- 英語予稿集(予稿集名) ------------------------
 
−
%\bibitem{M12+MATSUI4}
 
−
%  D. S. Johnson,
 
−
%  ``Fast Allocation Algorithms,''
 
−
%  in {\it Proceedings of the Thirteenth Annual Symposium  on Switching and Automata Theory},
 
−
%  144--154, 1972.
 
−
%--------------------------- 英語予稿集(会議名) --------------------------
 
−
%\bibitem{M12+MATSUI5}
 
−
%  M. X. Goemans and D. P. Williamson,              % 会議名は省略形も可
 
−
%  ``.878-Approximation Algorithms for MAX CUT and MAX2SAT,''
 
−
%  {\it STOC}, Canada, 422--431, 1984.              % 場所は国名程度
 
−
%--------------------------- 翻訳アリ ------------------------------------
 
−
%\bibitem{M12+MATSUI6}
 
−
%  E. W. Cheney,
 
−
%  ``Introduction to Approximation Theory,''
 
−
%  McGraw-Hill, 1966.                              % 最後はピリオド
 
−
%  一松信, 新島耕一 訳,
 
−
%  『近似理論入門』,
 
−
%  共立出版, 1977. 
 
−
%------------------------- 翻訳本 ---------------------------------------
 
−
%\bibitem{M12+MATSUI7}
 
−
%  国沢清典監訳,
 
−
%  『確率論とその応用II』,
 
−
%  紀ノ国屋書店, 1970.
 
−
%-------------------------- 日本語文献(和名雑誌)-----------------------
 
−
%\bibitem{M12+MATSUI8}
 
−
%  伊理正夫, 久保田光一,                              %
 
−
%  「高速自動微分法(I)(II)」,                        % 論文は「…」
 
−
%  『応用数理』,                                      % 雑誌は『…』
 
−
%  {\bf 1} (1991), 17--35, 153--163.
 
−
%-------------------------- 日本語文献(欧名雑誌)-----------------------
 
−
%\bibitem{M12+MATSUI9}
 
−
%  大沢義明, 鈴木敦夫,                                   
 
−
%  「グループ利用施設の最適配置とその頑健性について」, 
 
−
%  {\it Journal of the Operations Research Society of Japan},
 
−
%  {\bf 30} (1987), 368--395. 
 
−
%--------------------------- 日本語単行本(欧名交じり)-------------------
 
−
%\bibitem{M12+MATSUI10}
 
−
%  D. Avis, 今井浩, 松永信介,
 
−
%  『計算幾何学・離散幾何学』,
 
−
%  朝倉書店, 1994.
 
−
%--------------------------- 日本語単行本(監修と編集)-------------------
 
−
%\bibitem{M12+MATSUI11}
 
−
%  伊理正夫監修, 腰塚武志編集,
 
−
%  『計算幾何学と地理情報処理(第２版)』,
 
−
%  共立出版株式会社, 1993.
 
−
%--------------------------- 日本語予稿集(予稿集名) -----------------------
 
−
%\bibitem{M12+MATSUI12}
 
−
%  鈴木敦夫, 伊理正夫,
 
−
%  「駅の位置決め問題--利用者の費用最小」,
 
−
%  『日本オペレーションズ・リサーチ学会1986年春季研究発表会アブストラクト集』,
 
−
%  210--146, 1986.
 
−
%--------------------------- 日本語予稿集(会議名) -------------------------
 
−
%\bibitem{M12+MATSUI13}
 
−
%  鈴木敦夫,
 
−
%  「地理的最適化問題」,
 
−
%  日本オペレーションズ・リサーチ学会第13回シンポジウム,
 
−
%  25--28, 1984.
 
−
%---------------------------------------------------------------------------
 
  
−
%\end{thebibliography}
 
  
−
\end{document}
+
<center><table><tr><td align=center>[[画像:sk-0123-b-b-01-2.png]]</td></tr>
 +
<td align=center>図４：セントラルサーバモデル<br>
 +
</td></table></center>
 +
 
 +
<!--
 +
\begin{figure}[htbp] \begin{center} %\includegraphics[bbllx=0, bblly=210mm, bburx=230mm, bbury=260mm, %height=40mm]{. . /b-b/central.eps} \setlength{\unitlength}{1mm} \begin{picture}(72, 33)(0, -13) \thicklines \put(0, -1){\vector(1, 0){10}} \put(0, -1){\line(0, 1){21}} \put(0, 20){\line(1, 0){72}} \put(72, 0){\line(0, 1){20}} \put(62, 0){\line(1, 0){10}} \put(6, 1){\vector(1, 0){4}} \put(6, 1){\line(0, 1){7}} \put(6, 8){\line(1, 0){23}} \put(29, 0){\vector(0, 1){8}} \multiput(11, -2.5)(0, 5){2}{\line(1, 0){7}} \put(18, -2.5){\line(0, 1){5}} \put(18, 0){\line(1, 0){2}} \put(23, 0){\circle{6}} \put(26, 0){\line(1, 0){12}} \put(38, -10){\line(0, 1){20}} \put(38, 10){\vector(1, 0){5}} \multiput(44, 7.5)(0, 5){2}{\line(1, 0){7}} \put(51, 7.5){\line(0, 1){5}} \put(51, 10){\line(1, 0){2}} \put(56, 10){\circle{6}} \put(59, 10){\line(1, 0){3}} \put(38, -10){\vector(1, 0){5}} \multiput(44, -7.5)(0, -5){2}{\line(1, 0){7}} \put(51, -7.5){\line(0, -1){5}} \put(51, -10){\line(1, 0){2}} \put(56, -10){\circle{6}} \put(59, -10){\line(1, 0){3}} \put(62, -10){\line(0, 1){20}} \put(48, 0){\makebox(0, 1.2){\Huge $\vdots$}} \end{picture} \caption{セントラルサーバモデル}\label{B-B-01+central-server-model} \end{center} \end{figure}  
 +
-->
 +
 
 +
 
 +
　また単一待ち行列モデルで客の母集団が有限である場合も, 閉鎖型ネットワークの一例と見ることも可能である.
 +
　さらに客が優先権，待ち行列ネットワーク内の移動経路などの属性により複数クラスに分類され，一部のクラスに属する客に関しては開放型で，他のクラス
 +
の客に関しては閉鎖型のネットワークを[[混合型待ち行列ネットワーク]]と呼ぶ．
 +
　待ち行列ネットワークの別の分類として，各ノードで許容される待ち行列長に関する制限の有無に依るものがある．制限が無い場合には適当なモデル化の仮
 +
定を設ければ積形式解を用いた実用的な計算が可能であるが，制限がある場合には，ブロッキングが発生し，ノード間のより一層複雑な従属性が生じ，有効な解析法は存在しない．このような場合には近似的なアプローチを取らざるを得ない．ブロッキングとは，次に訪問するノードの待合室が一杯のときに移動が妨げられることを言う．この結果，モデルによっては元のサーバが次の客へのサービスを行なえない．客がいるにも拘わらずサービスが開始されない．これは例えば多段工程からなる生産ラインにおける，各工程における仕掛品置き場のように大容量のバッファがないシステムに相当する．一方通信網においては，ブロッキングが発生すると客であるパケット・メッセージなどは消滅する．
 +
　待ち行列ネットワークは，従来単一待ち行列システムでモデル化されていた生産・通信・コンピュータ・輸送・交通システムのネットワーク化に伴い，その
 +
重要性が増しており，特に積形式解を持つモデルの数値計算を支援するソフトウェア・パッケージなども提供されている．
 +
 
 +
[[category:待ち行列|まちぎょうれつもでるえむえむしー]]
 +
 
 +
[[category:待ち行列ネットワーク|まちぎょうれつねっとわーく]]
 +
 
 +
[[category:待ち行列の応用|まちぎょうれつのつうしんへのおうよう]]

2008年11月13日 (木) 22:00時点における最新版

【まちぎょうれつねっとわーく (queueing network)】

概要

複数の待ち行列システムが，直列，リング状あるいはネットワーク状に組み合わされた数学モデル．情報ネットワーク，コンピュータシステム，FMS（flexible manufacturing system）を始めとする生産システム，交通システムなどの複合システムにおける「待ち」現象の確率的振る舞いを取り扱う．待ち時間，待ち行列長，スループットなどの性能評価量を算出するのに用いられる．

詳説

　複数の待ち行列システム(以下ノードと表記)が, 図1のようにネットワーク上に結合された数学モデルを待ち行列ネットワーク (queueing network あるいは network of queues) と呼ぶ.


図１：待ち行列ネットワーク
図１：待ち行列ネットワーク


　各ノード間の移動は通常確率的に選択される. 例えばノード から は確率 で移動する. 経路選択確率 (routing probability) あるいは分岐確率 (branching probability) と呼ぶ. 特にネットワーク外を表現するのにノード0と記す．このモデルの確率的な振る舞いを解析し, 待ち時間・待ち行列長・スループットなどに関する性能評価量を算出が可能となる. 特に図2のように直列につながったモデルを直列型待ち行列(queueing networkあるいはnetwork of queues)と呼ぶ．

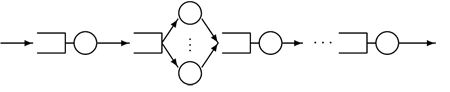Sk-0123-b-b-01-1.png
図２：直列型待ち行列


　これらのモデルにおいては，あるノードからの退去過程は他のノードへの到着過程になることからノード間の従属性が生じる．さらにはネットワークにフィー ドバック・ループがある場合には，退去した客が再度到着する可能性もあり，到着客間にも従属性が生じる．これらのことから個別のノードを取り出し，解 析するのは不可能であり，ネットワーク全体を捉えた解析が必要である．これまでに解析的にはマルコフ性を保持しながら，積形式解が得られる範囲内で，現実のシステムにより近いモデルが次々と発表されて来た． 　待ち行列ネットワークは，外部との関わり方で開放型ネットワーク(open network)と閉鎖型ネットワーク(closed network)に分類が可能である．開放型ネットワークにおいてはネットワーク外からの客の到着があり，またネットワーク外への退去もある．従ってネットワーク内の総客数は可変であり，一定ではない．これは例えば蓄積交換型のパケット交換網においては，パケット送信要求の発生が客のネットワークへの流入に相当し，各交換機およびそれに付随するバッファが各ノードに対応する．従って目的局に受信されることが，ネットワークからの退去に当たる．一方閉鎖型ネットワークにおいてはネットワーク外からの客の到着，外への退去はない．従って総客数が常に一定に保たれる．これは例えば一定台数の機械から構成されるシステムにおいて機械の故障・修理を考慮した性能評価を行なう際に用いられる．あるいはマルチプログラミング環境下で動作する計算機システムのように，内部にCPU，I/O機器などのサーバおよびそれに付随した待ち行列があり，総客数は一定に保たれている場合に相当する．計算が完了したジョブ／トランザクションはネットワークから消滅するが，それと同時にネットワーク外のバッファに貯えられていたジョブ・トランザクションが投入され，結果として総数が変わらないような場合にも適用が可能であり，計算機アーキテクチュアなどの評価に用いられた．閉鎖型ネットワークで，機械修理問題に見られるように，稼動状態，修理待ち状態，検査待ち状態のそれぞれに対応するノードを順番に訪問し，客の流れが同一方向で，訪問する待ち行列の順番が一定な直列型待ち行列を特に循環型待ち行列(図3参照)と呼ぶ．



図３：循環型待ち行列

図３：循環型待ち行列


　また図4に示すように, 計算機システムをモデル化した閉鎖型ネットワークで, 中央に位置するサーバ (CPU に相当) と複数の他のサーバおよびそれに付随する待ち行列 (入出力機器などの周辺機器に相当) からなり, 客がこれらの間を交互に行き来するモデルをセントラルサーバモデルと呼ぶ.


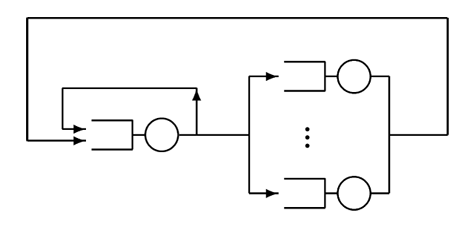Sk-0123-b-b-01-2.png
図４：セントラルサーバモデル


　また単一待ち行列モデルで客の母集団が有限である場合も, 閉鎖型ネットワークの一例と見ることも可能である. 　さらに客が優先権，待ち行列ネットワーク内の移動経路などの属性により複数クラスに分類され，一部のクラスに属する客に関しては開放型で，他のクラス の客に関しては閉鎖型のネットワークを混合型待ち行列ネットワークと呼ぶ． 　待ち行列ネットワークの別の分類として，各ノードで許容される待ち行列長に関する制限の有無に依るものがある．制限が無い場合には適当なモデル化の仮 定を設ければ積形式解を用いた実用的な計算が可能であるが，制限がある場合には，ブロッキングが発生し，ノード間のより一層複雑な従属性が生じ，有効な解析法は存在しない．このような場合には近似的なアプローチを取らざるを得ない．ブロッキングとは，次に訪問するノードの待合室が一杯のときに移動が妨げられることを言う．この結果，モデルによっては元のサーバが次の客へのサービスを行なえない．客がいるにも拘わらずサービスが開始されない．これは例えば多段工程からなる生産ラインにおける，各工程における仕掛品置き場のように大容量のバッファがないシステムに相当する．一方通信網においては，ブロッキングが発生すると客であるパケット・メッセージなどは消滅する． 　待ち行列ネットワークは，従来単一待ち行列システムでモデル化されていた生産・通信・コンピュータ・輸送・交通システムのネットワーク化に伴い，その 重要性が増しており，特に積形式解を持つモデルの数値計算を支援するソフトウェア・パッケージなども提供されている．

「https://orsj-ml.org/orwiki/wiki/index.php?title=待ち行列ネットワーク&oldid=11025」から取得