「《CAPM》」の版間の差分
| 2行目: | 2行目: | ||
CAPMは資本資産評価モデルとよばれ,資本市場の均衡下において危険資産のリス | CAPMは資本資産評価モデルとよばれ,資本市場の均衡下において危険資産のリス | ||
| − | + | クプレミアムがどのように決定されるかを説明するモデルである.このモデルはSharpe | |
| − | (1964),Linmer(1965),Mossin(1966) | + | (1964),Linmer(1965),Mossin(1966)によって提案された.いずれのモデルも危険資産 |
の投資収益を基準に議論を行うが,Sharpe-Lintner 型 CAPMはで投資比率によってポー | の投資収益を基準に議論を行うが,Sharpe-Lintner 型 CAPMはで投資比率によってポー | ||
トフォリオを定義し,リスクリターン平面上の無差別曲線を使って最適ポートフォリオ | トフォリオを定義し,リスクリターン平面上の無差別曲線を使って最適ポートフォリオ | ||
を考察するのに対し,Mossin 型 CAPMでは証券の保有枚数によってポートフォリオを | を考察するのに対し,Mossin 型 CAPMでは証券の保有枚数によってポートフォリオを | ||
| − | 定義し, | + | 定義し,投資家の効用関数から直接的に最適ポートフォリオを導出する点が異なる.本 |
| − | 項目ではSharpe-Lintner 型 | + | 項目ではSharpe-Lintner 型 CAPMを中心に説明を行う. |
■ 市場均衡 | ■ 市場均衡 | ||
CAPMは投資家の行動原理としてMarkoWitz(1952)のポートフォリオ選択(平均・分 | CAPMは投資家の行動原理としてMarkoWitz(1952)のポートフォリオ選択(平均・分 | ||
| − | 散モデル) | + | 散モデル)を利用している.したがって,CAPMではポートフォリオ選択の以下の仮定 |
| − | + | を引き継ぐことになる. | |
| − | + | ① 1期間だけの投資を考える. | |
| − | ② 投資家は投資収益率の平均および分散のみを考え, | + | ② 投資家は投資収益率の平均および分散のみを考え,期待効用を最大化する. |
| − | + | ③ すべての資産は無限に分割可能である. | |
④ 投資家はプライステーカーとして行動する. | ④ 投資家はプライステーカーとして行動する. | ||
| − | + | ⑤ 市場に摩擦はない.(取引コストや税金は存在しない.) | |
| − | + | さらにCAPMでは次の2つの仮定を加える. | |
⑥ 投資収益の同時分布についての予想は,すべての投資家で一致している. | ⑥ 投資収益の同時分布についての予想は,すべての投資家で一致している. | ||
| − | ⑦ 安全資産が1つ存在し, | + | ⑦ 安全資産が1つ存在し,無制限に貸借可能である. |
この仮定⑥は投資家の同質的期待とよばれ,すべての投資家はリスクリターン平面上 | この仮定⑥は投資家の同質的期待とよばれ,すべての投資家はリスクリターン平面上 | ||
| − | + | で同じ投資機会集合と同じ効率的フロンティアをみていることを保証する. | |
さて,安全資産が存在するときには効率的フロンティアの外にまで投資機会集合は拡 | さて,安全資産が存在するときには効率的フロンティアの外にまで投資機会集合は拡 | ||
| − | れ, | + | れ,図1が示すリスクリターン平面上ではグレーの領域になる.この投資機会集合 |
の左上に位置する境界は投資家にとって最も効率的な投資が行えるポートフォリオの集合 | の左上に位置する境界は投資家にとって最も効率的な投資が行えるポートフォリオの集合 | ||
| − | であり,これを資本市場線(Capital Market Line; CML) | + | であり,これを資本市場線(Capital Market Line; CML)とよぶ. |
<center>[[画像:figure1.jpg|center]]</center> | <center>[[画像:figure1.jpg|center]]</center> | ||
| 45行目: | 45行目: | ||
このCMLは安全資産<math>r</math>とそこから効率的フロンティアに引いた接点<math>M</math>との | このCMLは安全資産<math>r</math>とそこから効率的フロンティアに引いた接点<math>M</math>との | ||
| − | 組み合わせでつくられることから, | + | 組み合わせでつくられることから,次式が与えられる. |
| 54行目: | 54行目: | ||
ただし、<math>\mu_P</math>はCML上にあるポートフォリオの期待リターン,<math>\sigma_P</math> | ただし、<math>\mu_P</math>はCML上にあるポートフォリオの期待リターン,<math>\sigma_P</math> | ||
| − | + | はそのリスクである. | |
| − | + | 合理的な投資家はCML上のポートフォリオを保有する.すなわち、接点ポートフォリオ | |
| − | <math>M</math> | + | <math>M</math>と安全資産の2資産のみを保有することになる.これを2資産分離とよぶ. |
| − | + | 投資家による選好の違いはこの2資産への配分比率にのみ現れる.このように,投資家の効用とは | |
独立に危険資産ポートフォリオ<math>M</math>が決定されることをポートフォリオ選択における | 独立に危険資産ポートフォリオ<math>M</math>が決定されることをポートフォリオ選択における | ||
| − | + | 分離定理とよぶ. | |
| − | + | 次に市場の均衡を考えてみよう.市場の均衡とは,すべての資産についていかなる超過需要も | |
| − | + | 超過供給も存在しない状態である.このとき,投資家は自らが希望する危険資産ポートフォリオ | |
| − | <math>M</math>をすでに保有しており,かつ, | + | <math>M</math>をすでに保有しており,かつ,いかなる余剰資産も保有していない. |
また市場全体について考えてみると,いかなる資産についても超過需要,超過供給が | また市場全体について考えてみると,いかなる資産についても超過需要,超過供給が | ||
存在しないということは,すべての危険資産はその時価総額の比率でポートフォリオ | 存在しないということは,すべての危険資産はその時価総額の比率でポートフォリオ | ||
| − | <math>M</math> | + | <math>M</math>に含まれていることになる.したがって,市場の均衡状態においては, |
| − | ポートフォリオ<math>M</math> | + | ポートフォリオ<math>M</math>は時価総額加重の危険資産ポートフォリオに一致する. |
このようなポートフォリオは,面倒な効率的フロンティアの計算や接点を求めることなしに, | このようなポートフォリオは,面倒な効率的フロンティアの計算や接点を求めることなしに, | ||
| − | + | 直接的に市場で観測することができる.このポートフォリオ<math>M</math>は危険資産市場を | |
| − | 代表する投資化共通の最適ポートフォリオであるから, | + | 代表する投資化共通の最適ポートフォリオであるから,これを市場ポートフォリオとよぶ. |
なお,数ある市場インデックスの中で時価総額加重インデックスが理論上優れていると | なお,数ある市場インデックスの中で時価総額加重インデックスが理論上優れていると | ||
| − | いわれるのは, | + | いわれるのは,この市場ポートフォリオの特性による. |
| − | さて, | + | さて,市場ポートフォリオと個別資産の関係を見てみよう.資産<math>i</math>と市場ポートフォリオ |
| − | <math>M</math> | + | <math>M</math>とで新たにつくられる超過ポートフォリオの奇跡を描くと図2のようになる. |
| 83行目: | 83行目: | ||
超過ポートフォリオの軌跡とCMLが点Mで接することから,次の証券市場線(Security Market Line; SML) | 超過ポートフォリオの軌跡とCMLが点Mで接することから,次の証券市場線(Security Market Line; SML) | ||
| − | + | が導かれる. | |
| 97行目: | 97行目: | ||
</center> | </center> | ||
| − | + | である. | |
式(2)は個別資産の期待リターンが安全利子率とリスクプレミアムに分解されること | 式(2)は個別資産の期待リターンが安全利子率とリスクプレミアムに分解されること | ||
| − | + | を示している.また,リスクプレミアムは市場の超過収益(市場のリスクプレミアム)を | |
<math>\beta_i</math>倍したものになっており,この<math>\beta_i</math>がリスクプレミアムの大小を決める重要なパラメー | <math>\beta_i</math>倍したものになっており,この<math>\beta_i</math>がリスクプレミアムの大小を決める重要なパラメー | ||
| − | + | タとなる.式(3)は<math>\beta_i</math>の定義を示しているが,これは市場ポートフォリオと個別資産の | |
| − | 投資収益率の共分散によって<math>\beta_i</math> | + | 投資収益率の共分散によって<math>\beta_i</math>が決定される.すなわち,これはシステマティックリ |
| − | スクであり, | + | スクであり,分散投資によって除去することのできないリスクである.市場は分散不可 |
能なシステマティックリスクにのみリスクプレミアムを支払い,分散投資により消去可 | 能なシステマティックリスクにのみリスクプレミアムを支払い,分散投資により消去可 | ||
| − | + | 能なアンシステマティックリスクに対してはプレミアムを支払わないのである.これが | |
| − | + | CAPMの結論である. | |
| − | なお, | + | なお,SMLを図示すると図3のようになる. |
| 116行目: | 116行目: | ||
<math>\beta = 1</math>の資産はシステマティックリスクの大きさが市場ポートフォリオと一致し,した | <math>\beta = 1</math>の資産はシステマティックリスクの大きさが市場ポートフォリオと一致し,した | ||
| − | + | がって期待リターンも市場ポートフォリオの期待リターンに一致する.<math>\beta</math>が1より小さ | |
い資産は市場よリローリスクローリターンであり防御的銘柄,<math>\beta</math>が1より大きい資産は | い資産は市場よリローリスクローリターンであり防御的銘柄,<math>\beta</math>が1より大きい資産は | ||
市場よリハイリスクハイリターンで攻撃的銘柄と分類される. | 市場よリハイリスクハイリターンで攻撃的銘柄と分類される. | ||
| 123行目: | 123行目: | ||
■ ゼロベータCAPM | ■ ゼロベータCAPM | ||
| − | Black(1972) | + | Black(1972)は安全資産が存在しない場合の均衡モデルを提案した.効率的フロンティ |
アの数学的特徴から,フロンティア上にある任意のポートフォリオに対して,相関がゼ | アの数学的特徴から,フロンティア上にある任意のポートフォリオに対して,相関がゼ | ||
ロ,すなわちベータがゼロとなるポートフオリオが同じ効率的フロンテイア上に必ず存在 | ロ,すなわちベータがゼロとなるポートフオリオが同じ効率的フロンテイア上に必ず存在 | ||
| − | + | する.したがって,市場ポートフォリオMが効率的フロンテイア上にあるならば,それ | |
に対するゼロベータポートフォリオZを安全資産のかわりに用いることにより,CAPM | に対するゼロベータポートフォリオZを安全資産のかわりに用いることにより,CAPM | ||
| − | + | が成立する.これをゼロベータCAPMあるいはBlackモデルとよぶ. | |
<center>[[画像:figure4.jpg|center]]</center> | <center>[[画像:figure4.jpg|center]]</center> | ||
| 146行目: | 146行目: | ||
</center> | </center> | ||
| − | + | である. | |
| 155行目: | 155行目: | ||
(1973)などがある.その実証手続きは主に以下のようなものである. | (1973)などがある.その実証手続きは主に以下のようなものである. | ||
| − | Step1 | + | Step1 市場ポートフオリオの代理変数として適切な市場インデックスを1つ定める. |
| − | Step2 市場インデックス,個別株式, | + | Step2 市場インデックス,個別株式,安全資産の月次収益率を収集する. |
Step3 月々の投資収益率からその月の安全利子率を差し引いた超過収益率を求める. | Step3 月々の投資収益率からその月の安全利子率を差し引いた超過収益率を求める. | ||
Step4 個別株式の超過収益と市場インデックスの超過収益で単回帰(時系列回帰)し, | Step4 個別株式の超過収益と市場インデックスの超過収益で単回帰(時系列回帰)し, | ||
| − | 各株式の<math>\beta</math> | + | 各株式の<math>\beta</math>値を計測する. |
| − | Step5 <math>\beta</math> | + | Step5 <math>\beta</math>の大小によリランキングされた20銘柄程度のポートフォリオを作成する. |
Step6 ポートフオリオの期待収益率を<math>\beta</math>値で単回帰(横断回帰)することで,SMLを | Step6 ポートフオリオの期待収益率を<math>\beta</math>値で単回帰(横断回帰)することで,SMLを | ||
| 170行目: | 170行目: | ||
彼らの検証結果によるとSMLの傾きはややフラットであるものの,概ねCAPMは支 | 彼らの検証結果によるとSMLの傾きはややフラットであるものの,概ねCAPMは支 | ||
| − | + | 持された.しかし,このような検証方法に対してRoll(1977)により大きな疑問点が提 | |
| − | + | 示された.その要旨は以下のようなものである.BlackのゼロベータCAPMが示すよう | |
に,SMLの成立は市場ポートフォリオが効率的フロンティア上にあることと同値であ | に,SMLの成立は市場ポートフォリオが効率的フロンティア上にあることと同値であ | ||
| − | + | る.しかし,これまでの検証では市場ポートフォリオの代理変数として市場インデック | |
| − | + | スが用いられる.したがって,これまでの実証分析は分析に用いられた市場インデック | |
| − | スの効率性を検証していることにほかならず, | + | スの効率性を検証していることにほかならず,これはCAPMの検証とは無関係である. |
真の市場ポートフォリオが用いられないかぎり,本当のCAPMの検証とはなりえない. | 真の市場ポートフォリオが用いられないかぎり,本当のCAPMの検証とはなりえない. | ||
しかし,市場ポートフォリオはその性質上,投資可能なあらゆる危険資産を含まなけれ | しかし,市場ポートフォリオはその性質上,投資可能なあらゆる危険資産を含まなけれ | ||
| − | + | ばならない.株式や債券のみならず実物資産や人的資本を含むすべての危険資産の構成 | |
| − | + | を巌密に調べるのは不可能である.したがって,CAPMの検証は原理的には可能だが実 | |
| − | + | 質的には不可能である. | |
このような批判を受けて,Ross(1976)はCAPMに代わる新しい資産評価理として | このような批判を受けて,Ross(1976)はCAPMに代わる新しい資産評価理として | ||
| − | 裁定価格理論(Arbitragc Pricing Theory;APT) | + | 裁定価格理論(Arbitragc Pricing Theory;APT)を提案した.CAPMが単一 |
ファクター(市場ポートフォリオ)モデルなのに対し,APTは複数ファクターモデルである.またAPTは | ファクター(市場ポートフォリオ)モデルなのに対し,APTは複数ファクターモデルである.またAPTは | ||
| − | 市場ポートフォリオの存在を前提としないため, | + | 市場ポートフォリオの存在を前提としないため,Rollの批判からは無縁である. |
このようなCAPMをめぐる論争の中,株式の期待投資収益率にはCAPMでは説明さ | このようなCAPMをめぐる論争の中,株式の期待投資収益率にはCAPMでは説明さ | ||
| − | + | れない有意な銘柄間格差があることが見つかつた.これをアノマリー現象とよぶ.Basu | |
(1977)は高い収益株価比率(EPR)をもつポートフォリオが高いリターンを示すことを発 | (1977)は高い収益株価比率(EPR)をもつポートフォリオが高いリターンを示すことを発 | ||
| − | + | 見した.Banz(1981)は投資収益率と株式の相対時価総額(規模の尺度)の間に統計的に | |
有意な負の関係があり,これが<math>\beta</math>の説明力を上回ることを発見した. Fama and French | 有意な負の関係があり,これが<math>\beta</math>の説明力を上回ることを発見した. Fama and French | ||
(1992)は株式の時価総額(規模の尺度)や株価純資産倍率(PBR)の逆数がリターンをうまく説明しており,市場インデックスに対する<math>\beta</math>に対して期待リターンはフラットである | (1992)は株式の時価総額(規模の尺度)や株価純資産倍率(PBR)の逆数がリターンをうまく説明しており,市場インデックスに対する<math>\beta</math>に対して期待リターンはフラットである | ||
| 198行目: | 198行目: | ||
プレミアムの発見への期待と絡んでさまざまな研究が行われているが,いまだはっきり | プレミアムの発見への期待と絡んでさまざまな研究が行われているが,いまだはっきり | ||
とした結論には至っていない.しかし,CAPMの検証結果が明確でないとしても,それ | とした結論には至っていない.しかし,CAPMの検証結果が明確でないとしても,それ | ||
| − | + | がCAPMの理論的な価値を下げるものではない.われわれが資本市場で行動する際に | |
| − | CAPMが提供してくれるリスクの概念は, | + | CAPMが提供してくれるリスクの概念は,その検証可能性とは無関係に有用なのである. |
| 205行目: | 205行目: | ||
1期間モデルであるCAPMを多期間あるいは連続時間へ拡張しようとするのは自然な | 1期間モデルであるCAPMを多期間あるいは連続時間へ拡張しようとするのは自然な | ||
| − | + | 流れである.このとき,1期間CAPMで導かれたリターンと<math>\beta</math>の線形関係が維持される | |
| − | + | かどうかが最大の論点となる. | |
| − | Merton(1973) | + | Merton(1973)は資産評価モデルに初めて連続時間のフレームワークを導入した.彼の |
ICAPM (Intertemporal CAPM)では連続的な資産の取引を想定し,第<math>i</math>資産の価格<math>P_i</math>が | ICAPM (Intertemporal CAPM)では連続的な資産の取引を想定し,第<math>i</math>資産の価格<math>P_i</math>が | ||
| − | + | 次の伊藤過程に従うものと仮定する. | |
| 219行目: | 219行目: | ||
ただし,<math>\mu_i</math>は資産<math>i</math>の期待収益率,<math>x</math>は状態変数,<math>\sigma^2_i</math>は | ただし,<math>\mu_i</math>は資産<math>i</math>の期待収益率,<math>x</math>は状態変数,<math>\sigma^2_i</math>は | ||
| − | + | 収益率の分散である. | |
また,状態変数<math>x</math>も1次元伊藤過程 | また,状態変数<math>x</math>も1次元伊藤過程 | ||
| 227行目: | 227行目: | ||
</center> | </center> | ||
| − | + | に従うものとする. | |
次に,投資家kは時点tにおける消費<math>c_{k,t}</math>から効用を得るものと考え,以下のよう | 次に,投資家kは時点tにおける消費<math>c_{k,t}</math>から効用を得るものと考え,以下のよう | ||
| − | + | な効用の時間積分の期待値を考える. | |
<center> | <center> | ||
| 237行目: | 237行目: | ||
この期待効用の最大化問題を解くことにより,最適ポートフォリオ戦略<math>w_k</math>は次のよ | この期待効用の最大化問題を解くことにより,最適ポートフォリオ戦略<math>w_k</math>は次のよ | ||
| − | + | うに導かれる. | |
<center> | <center> | ||
| 254行目: | 254行目: | ||
| − | + | である.ここで<math>A_k</math>は投資家kの相対リスク回避度(ARR),<math>\boldsymbol{V}</math>は資産の価格変化率の共 | |
分散行列,<math>H_k</math>は投資家kの状態変数<math>x</math>に対する選好を表すパラメータ,<math>\boldsymbol{\sigma}_x</math>は各資産変 | 分散行列,<math>H_k</math>は投資家kの状態変数<math>x</math>に対する選好を表すパラメータ,<math>\boldsymbol{\sigma}_x</math>は各資産変 | ||
| − | 化率と状態変数<math>x</math> | + | 化率と状態変数<math>x</math>との共分散ベクトルである.式(10)が示す<math>\boldsymbol{w}_T</math>は効率的フロンティア |
上の接点ポートフォリオであり,式(11)が示す<math>\boldsymbol{w}_H</math>は状態変数<math>x</math>との相関が最大となる | 上の接点ポートフォリオであり,式(11)が示す<math>\boldsymbol{w}_H</math>は状態変数<math>x</math>との相関が最大となる | ||
| − | + | ポートフォリオである.式(9)により3資産分離定理が導かれる.すなわち,投資家は | |
安全資産,接点ポートフォリオ<math>\boldsymbol{w}_r</math>,ヘッジポートフォリオ<math>\boldsymbol{w}_H</math>に投資するのである. | 安全資産,接点ポートフォリオ<math>\boldsymbol{w}_r</math>,ヘッジポートフォリオ<math>\boldsymbol{w}_H</math>に投資するのである. | ||
| 269行目: | 269行目: | ||
| − | ここで<math>\beta_{i,T}</math>は接点ポートフォリオとの<math>\beta</math>値,<math>\lambda_T</math>は接点ポートフォリオのリスクプレミアム(期待超過リターン),<math>\beta_{i,x}</math>は状態変数<math>x</math>に対するヘッジポートフォリオの<math>\beta</math>値,<math>\lambda_x</math> | + | ここで<math>\beta_{i,T}</math>は接点ポートフォリオとの<math>\beta</math>値,<math>\lambda_T</math>は接点ポートフォリオのリスクプレミアム(期待超過リターン),<math>\beta_{i,x}</math>は状態変数<math>x</math>に対するヘッジポートフォリオの<math>\beta</math>値,<math>\lambda_x</math>はヘッジポートフォリオのリスクプレミアムである. |
これまで状態変数<math>x</math>はスカラーであると仮定してきたが, これが<math>s</math>次元ベクトルであ | これまで状態変数<math>x</math>はスカラーであると仮定してきたが, これが<math>s</math>次元ベクトルであ | ||
| 280行目: | 280行目: | ||
| − | + | となる.このモデルはマルチベータモデルとも呼ばれる. | |
2007年8月8日 (水) 20:00時点における版
【きゃっぷえむ (Capital Asset Pricing Model)】
CAPMは資本資産評価モデルとよばれ,資本市場の均衡下において危険資産のリス クプレミアムがどのように決定されるかを説明するモデルである.このモデルはSharpe (1964),Linmer(1965),Mossin(1966)によって提案された.いずれのモデルも危険資産 の投資収益を基準に議論を行うが,Sharpe-Lintner 型 CAPMはで投資比率によってポー トフォリオを定義し,リスクリターン平面上の無差別曲線を使って最適ポートフォリオ を考察するのに対し,Mossin 型 CAPMでは証券の保有枚数によってポートフォリオを 定義し,投資家の効用関数から直接的に最適ポートフォリオを導出する点が異なる.本 項目ではSharpe-Lintner 型 CAPMを中心に説明を行う.
■ 市場均衡
CAPMは投資家の行動原理としてMarkoWitz(1952)のポートフォリオ選択(平均・分 散モデル)を利用している.したがって,CAPMではポートフォリオ選択の以下の仮定 を引き継ぐことになる.
① 1期間だけの投資を考える.
② 投資家は投資収益率の平均および分散のみを考え,期待効用を最大化する.
③ すべての資産は無限に分割可能である.
④ 投資家はプライステーカーとして行動する.
⑤ 市場に摩擦はない.(取引コストや税金は存在しない.)
さらにCAPMでは次の2つの仮定を加える.
⑥ 投資収益の同時分布についての予想は,すべての投資家で一致している.
⑦ 安全資産が1つ存在し,無制限に貸借可能である.
この仮定⑥は投資家の同質的期待とよばれ,すべての投資家はリスクリターン平面上 で同じ投資機会集合と同じ効率的フロンティアをみていることを保証する.
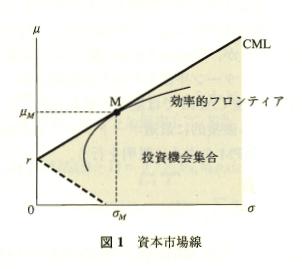
さて,安全資産が存在するときには効率的フロンティアの外にまで投資機会集合は拡 れ,図1が示すリスクリターン平面上ではグレーの領域になる.この投資機会集合 の左上に位置する境界は投資家にとって最も効率的な投資が行えるポートフォリオの集合 であり,これを資本市場線(Capital Market Line; CML)とよぶ.
このCMLは安全資産構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle r}
とそこから効率的フロンティアに引いた接点構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle M}
との
組み合わせでつくられることから,次式が与えられる.
構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \mu_P = r + \frac{\mu_M - r}{\sigma_M} \sigma_P \ \ \ (1)}
ただし、構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \mu_P}
はCML上にあるポートフォリオの期待リターン,構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \sigma_P}
はそのリスクである.
合理的な投資家はCML上のポートフォリオを保有する.すなわち、接点ポートフォリオ 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle M} と安全資産の2資産のみを保有することになる.これを2資産分離とよぶ. 投資家による選好の違いはこの2資産への配分比率にのみ現れる.このように,投資家の効用とは 独立に危険資産ポートフォリオ構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle M} が決定されることをポートフォリオ選択における 分離定理とよぶ.
次に市場の均衡を考えてみよう.市場の均衡とは,すべての資産についていかなる超過需要も 超過供給も存在しない状態である.このとき,投資家は自らが希望する危険資産ポートフォリオ 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle M} をすでに保有しており,かつ,いかなる余剰資産も保有していない. また市場全体について考えてみると,いかなる資産についても超過需要,超過供給が 存在しないということは,すべての危険資産はその時価総額の比率でポートフォリオ 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle M} に含まれていることになる.したがって,市場の均衡状態においては, ポートフォリオ構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle M} は時価総額加重の危険資産ポートフォリオに一致する. このようなポートフォリオは,面倒な効率的フロンティアの計算や接点を求めることなしに, 直接的に市場で観測することができる.このポートフォリオ構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle M} は危険資産市場を 代表する投資化共通の最適ポートフォリオであるから,これを市場ポートフォリオとよぶ. なお,数ある市場インデックスの中で時価総額加重インデックスが理論上優れていると いわれるのは,この市場ポートフォリオの特性による.
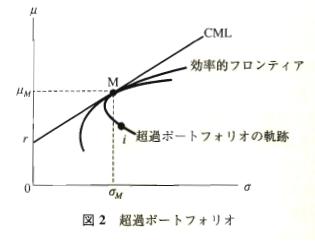
さて,市場ポートフォリオと個別資産の関係を見てみよう.資産構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle i} と市場ポートフォリオ 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle M} とで新たにつくられる超過ポートフォリオの奇跡を描くと図2のようになる.
超過ポートフォリオの軌跡とCMLが点Mで接することから,次の証券市場線(Security Market Line; SML)
が導かれる.
構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \mu_i = r + \beta_i (\mu_M - r) \ \ \ (2)}
ただし,
構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \beta_i = \frac{\mbox{Cov}_{i,M}}{\sigma^2_M} \ \ \ (3)}
である.
式(2)は個別資産の期待リターンが安全利子率とリスクプレミアムに分解されること を示している.また,リスクプレミアムは市場の超過収益(市場のリスクプレミアム)を 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \beta_i} 倍したものになっており,この構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \beta_i} がリスクプレミアムの大小を決める重要なパラメー タとなる.式(3)は構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \beta_i} の定義を示しているが,これは市場ポートフォリオと個別資産の 投資収益率の共分散によって構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \beta_i} が決定される.すなわち,これはシステマティックリ スクであり,分散投資によって除去することのできないリスクである.市場は分散不可 能なシステマティックリスクにのみリスクプレミアムを支払い,分散投資により消去可 能なアンシステマティックリスクに対してはプレミアムを支払わないのである.これが CAPMの結論である.
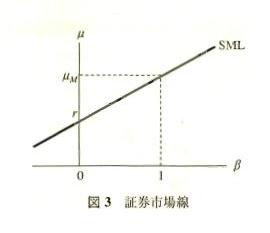
なお,SMLを図示すると図3のようになる.
構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \beta = 1}
の資産はシステマティックリスクの大きさが市場ポートフォリオと一致し,した
がって期待リターンも市場ポートフォリオの期待リターンに一致する.構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \beta}
が1より小さ
い資産は市場よリローリスクローリターンであり防御的銘柄,構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \beta}
が1より大きい資産は
市場よリハイリスクハイリターンで攻撃的銘柄と分類される.
■ ゼロベータCAPM
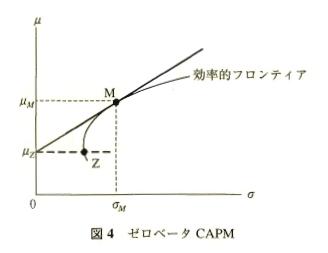
Black(1972)は安全資産が存在しない場合の均衡モデルを提案した.効率的フロンティ アの数学的特徴から,フロンティア上にある任意のポートフォリオに対して,相関がゼ ロ,すなわちベータがゼロとなるポートフオリオが同じ効率的フロンテイア上に必ず存在 する.したがって,市場ポートフォリオMが効率的フロンテイア上にあるならば,それ に対するゼロベータポートフォリオZを安全資産のかわりに用いることにより,CAPM が成立する.これをゼロベータCAPMあるいはBlackモデルとよぶ.
ゼロベータCAPMでは次のような証券市場線が導かれる.
構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \mu_i = \mu z + \beta_i (\mu_M - \mu z) \ \ \ (4)}
ただし,
構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \beta_i = \frac{\mbox{Cov}_{i,M}}{\sigma_M^2 } \ \ \ (5)}
である.
■ CAPMの検証
CAPMはその結論のシンプルさゆえ,古くから数多くの検証が行われてきた.その代表 的なものにBlack,Jensen and Scholes(1972), Blume and Fiend(1973), Fama and MacBeth (1973)などがある.その実証手続きは主に以下のようなものである.
Step1 市場ポートフオリオの代理変数として適切な市場インデックスを1つ定める.
Step2 市場インデックス,個別株式,安全資産の月次収益率を収集する.
Step3 月々の投資収益率からその月の安全利子率を差し引いた超過収益率を求める.
Step4 個別株式の超過収益と市場インデックスの超過収益で単回帰(時系列回帰)し, 各株式の構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \beta} 値を計測する.
Step5 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \beta} の大小によリランキングされた20銘柄程度のポートフォリオを作成する.
Step6 ポートフオリオの期待収益率を構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \beta} 値で単回帰(横断回帰)することで,SMLを 検証する.
彼らの検証結果によるとSMLの傾きはややフラットであるものの,概ねCAPMは支 持された.しかし,このような検証方法に対してRoll(1977)により大きな疑問点が提 示された.その要旨は以下のようなものである.BlackのゼロベータCAPMが示すよう に,SMLの成立は市場ポートフォリオが効率的フロンティア上にあることと同値であ る.しかし,これまでの検証では市場ポートフォリオの代理変数として市場インデック スが用いられる.したがって,これまでの実証分析は分析に用いられた市場インデック スの効率性を検証していることにほかならず,これはCAPMの検証とは無関係である. 真の市場ポートフォリオが用いられないかぎり,本当のCAPMの検証とはなりえない. しかし,市場ポートフォリオはその性質上,投資可能なあらゆる危険資産を含まなけれ ばならない.株式や債券のみならず実物資産や人的資本を含むすべての危険資産の構成 を巌密に調べるのは不可能である.したがって,CAPMの検証は原理的には可能だが実 質的には不可能である.
このような批判を受けて,Ross(1976)はCAPMに代わる新しい資産評価理として 裁定価格理論(Arbitragc Pricing Theory;APT)を提案した.CAPMが単一 ファクター(市場ポートフォリオ)モデルなのに対し,APTは複数ファクターモデルである.またAPTは 市場ポートフォリオの存在を前提としないため,Rollの批判からは無縁である.
このようなCAPMをめぐる論争の中,株式の期待投資収益率にはCAPMでは説明さ れない有意な銘柄間格差があることが見つかつた.これをアノマリー現象とよぶ.Basu (1977)は高い収益株価比率(EPR)をもつポートフォリオが高いリターンを示すことを発 見した.Banz(1981)は投資収益率と株式の相対時価総額(規模の尺度)の間に統計的に 有意な負の関係があり,これが構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \beta} の説明力を上回ることを発見した. Fama and French (1992)は株式の時価総額(規模の尺度)や株価純資産倍率(PBR)の逆数がリターンをうまく説明しており,市場インデックスに対する構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \beta} に対して期待リターンはフラットである ことを発見した.
現在もCAPMの検証をめぐる問題は,市場の効率性のチェックあるいは新たなリスク プレミアムの発見への期待と絡んでさまざまな研究が行われているが,いまだはっきり とした結論には至っていない.しかし,CAPMの検証結果が明確でないとしても,それ がCAPMの理論的な価値を下げるものではない.われわれが資本市場で行動する際に CAPMが提供してくれるリスクの概念は,その検証可能性とは無関係に有用なのである.
■ 連続時間モデル
1期間モデルであるCAPMを多期間あるいは連続時間へ拡張しようとするのは自然な 流れである.このとき,1期間CAPMで導かれたリターンと構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \beta} の線形関係が維持される かどうかが最大の論点となる.
Merton(1973)は資産評価モデルに初めて連続時間のフレームワークを導入した.彼の ICAPM (Intertemporal CAPM)では連続的な資産の取引を想定し,第構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle i} 資産の価格構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle P_i} が 次の伊藤過程に従うものと仮定する.
構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \frac{\mbox{d}P_i}{P_i} = \mu_i (x) \mbox{d}t + \sigma_i (x)\mbox{d} z_i \ \ \ (6)}
ただし,構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \mu_i}
は資産構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle i}
の期待収益率,構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle x}
は状態変数,構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \sigma^2_i}
は
収益率の分散である.
また,状態変数構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle x} も1次元伊藤過程
構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \mbox{d} x = m(x) \mbox{d} t + s(x) \mbox{d}z_x \ \ \ (7)}
に従うものとする.
次に,投資家kは時点tにおける消費構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle c_{k,t}} から効用を得るものと考え,以下のよう な効用の時間積分の期待値を考える.
構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \mbox{E} \Bigg[ \int_0^T u_k (c_{k,t} , x, t) \mbox{d}t \Bigg] \ \ \ (8)}
この期待効用の最大化問題を解くことにより,最適ポートフォリオ戦略構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle w_k} は次のよ うに導かれる.
構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \boldsymbol{w}_k = A_k [\boldsymbol{1}^T \boldsymbol{V}^{-1} (\mu - r\boldsymbol{1})]\boldsymbol{w}_T + H_k [\boldsymbol{1}^T \boldsymbol{V}^{-1} \boldsymbol{\sigma}_x]\boldsymbol{w}_H \ \ \ (9)}
ただし,
構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \boldsymbol{w}_T = \frac{\boldsymbol{V}^{-1} (\mu -r\boldsymbol{1})}{\boldsymbol{1}^T \boldsymbol{V}^{-1} (\mu - r\boldsymbol{1}) } \ \ \ (10)}
構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \boldsymbol{w}_H = \frac{\boldsymbol{V}^{-1} \boldsymbol{\sigma}_x}{\boldsymbol{1}^T \boldsymbol{V}^{-1} \boldsymbol{\sigma}_x } \ \ \ (11)}
である.ここで構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle A_k}
は投資家kの相対リスク回避度(ARR),構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \boldsymbol{V}}
は資産の価格変化率の共
分散行列,構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle H_k}
は投資家kの状態変数構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle x}
に対する選好を表すパラメータ,構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \boldsymbol{\sigma}_x}
は各資産変
化率と状態変数構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle x}
との共分散ベクトルである.式(10)が示す構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \boldsymbol{w}_T}
は効率的フロンティア
上の接点ポートフォリオであり,式(11)が示す構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \boldsymbol{w}_H}
は状態変数構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle x}
との相関が最大となる
ポートフォリオである.式(9)により3資産分離定理が導かれる.すなわち,投資家は
安全資産,接点ポートフォリオ構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \boldsymbol{w}_r}
,ヘッジポートフォリオ構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \boldsymbol{w}_H}
に投資するのである.
最後にICAPMが導く期待リターンとリスクプレミアムの関係式を示そう.
構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \mu_i = r + \beta_{i,T} \lambda_T + \beta_{i,x} \lambda_x \ \ \ (12)}
ここで構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \beta_{i,T}}
は接点ポートフォリオとの構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \beta}
値,構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \lambda_T}
は接点ポートフォリオのリスクプレミアム(期待超過リターン),構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \beta_{i,x}}
は状態変数構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle x}
に対するヘッジポートフォリオの構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \beta}
値,構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \lambda_x}
はヘッジポートフォリオのリスクプレミアムである.
これまで状態変数構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle x} はスカラーであると仮定してきたが, これが構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle s} 次元ベクトルであ る場合には,
構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \mu_i = r + \beta_{i,T} \lambda_T + \sum_{x=1}^s \beta_{i,x} \lambda_x \ \ \ (13)}
となる.このモデルはマルチベータモデルとも呼ばれる.
参考文献
[1] Black,F.(1972),"Capital market equilibrium with restricted borrowing," Journal of Business,45,444-455.
[2] Black,F.,M.C. Jensen and M.Scholes (1972), "The capital asset pricing model: Some empirical tests," in Jensen,M.C. ed., Studies inTheory of Capital Markets, Praeger.
[3] Blume,M.E. and I.Friend (1973),"A new look at the capital asset pricing model," Journal of Finance, 28, 19-33.
[4] Fama, E.F. and J. MacBeth (1973), "Rish return, and equilibrium: Empirical Tests:" Journal of Polititcal Economy,81.
[5] Fama E.F. and K.R. French (1992), "The cross section of expected stock returns," Journal of Finance, 47, 427-466.
[6] Lintner, J. (1965), "Ihe valuation of risky assets and the selection of risky assets and the selection of risky investments in stock portfolios and capital budgets,"Review of Economics and Statistics, 47, 13-37.
[7] Merton, R. (1973), "An intertemporal capital asset pricing model," Econometrica, 4l, 867-887.
[8] Mossin, J. (1966), "Equilibrium in a capital asset market," Econometrica, 34, 768-783.
[9] Roll, R. (1977), "A critique of the asset pricing theory's tests : Part I : On past and potential testability of the theory," Journal of Financial Economics, 4.
[10] Ross,R. (19?6), "the arbitrage theory of capital asset pricing," Journal of Economic Theory, l3.
[11] Sharpe,W.F. (1964), "Capital asset prices: A theory of market equilibrium under conditions of risk," Journal of Finance, 19, 425-442.