「《ラインバランシング》」の版間の差分
| 32行目: | 32行目: | ||
| − | + | <center> | |
| + | <math> | ||
\sum_{i \in S(k)}{e_i} \le {c}, \ \ \ k = 1, 2, \ldots , n | \sum_{i \in S(k)}{e_i} \le {c}, \ \ \ k = 1, 2, \ldots , n | ||
\, </math> <math>(1)\, </math> | \, </math> <math>(1)\, </math> | ||
| + | </center> | ||
| 40行目: | 42行目: | ||
| − | + | <center> | |
| + | <math> | ||
d_k = c - t_k, \ \ \ k = 1, 2, \ldots , n | d_k = c - t_k, \ \ \ k = 1, 2, \ldots , n | ||
\, </math> <math>(2)\, </math> | \, </math> <math>(2)\, </math> | ||
| + | </center> | ||
| 48行目: | 52行目: | ||
| − | + | <center> | |
| + | <math> | ||
T_w = \sum_{i = 1}^m e_i | T_w = \sum_{i = 1}^m e_i | ||
\, </math> <math>(3)\, </math> | \, </math> <math>(3)\, </math> | ||
| + | </center> | ||
| 56行目: | 62行目: | ||
| − | + | <center> | |
| + | <math> | ||
BD = \frac{\sum_{k = 1}^n {(c - t_k)}}{nc} \times 100 = \frac{nc - | BD = \frac{\sum_{k = 1}^n {(c - t_k)}}{nc} \times 100 = \frac{nc - | ||
T_w}{nc} \times 100 | T_w}{nc} \times 100 | ||
\, </math> <math>(4)\, </math> | \, </math> <math>(4)\, </math> | ||
| + | </center> | ||
| 65行目: | 73行目: | ||
| − | + | <center> | |
| + | <math> | ||
E = \frac{T_w}{nc} \times 100 | E = \frac{T_w}{nc} \times 100 | ||
\, </math> <math>(5)\, </math> | \, </math> <math>(5)\, </math> | ||
| + | </center> | ||
| 79行目: | 89行目: | ||
| − | + | <center> | |
| + | <math> | ||
L_i = \sum_{j=1}^{N}f_j\delta_{ij}e_i, \ \ \ i = 1, 2, \ldots , m | L_i = \sum_{j=1}^{N}f_j\delta_{ij}e_i, \ \ \ i = 1, 2, \ldots , m | ||
\, </math> <math>(6)\, </math> | \, </math> <math>(6)\, </math> | ||
| + | </center> | ||
| 87行目: | 99行目: | ||
| − | + | <center> | |
| + | <math> | ||
\sum_{i \in S(k)}L_i \le T, \ \ \ k = 1, 2, \ldots , n | \sum_{i \in S(k)}L_i \le T, \ \ \ k = 1, 2, \ldots , n | ||
\, </math> <math>(7)\, </math> | \, </math> <math>(7)\, </math> | ||
| + | </center> | ||
| 95行目: | 109行目: | ||
| − | + | <center> | |
| + | <math> | ||
E = \frac{\sum_i L_i}{nc \sum_j f_j} \times 100 = \frac{\sum_i | E = \frac{\sum_i L_i}{nc \sum_j f_j} \times 100 = \frac{\sum_i | ||
L_i}{nT} \times 100 | L_i}{nT} \times 100 | ||
\, </math> <math>(8)\, </math> | \, </math> <math>(8)\, </math> | ||
| − | + | </center> | |
2007年7月17日 (火) 14:51時点における版
【らいんばらんしんぐ (line balancing) 】
1. 概観
ラインバランスは本来生産ラインのワークステーション間での能力あるいは負荷の均等化を意味しており, 機械加工ラインと組立ラインの双方に望まれる特性として考えられてきた. しかし, その方法は両者の間で隔たりがあり, 機械加工の場合は機械の加工速度の差が問題になることが多く, 操業時間の調整や工程間在庫の保有によって, 組立作業の場合は作業の分割, 組合せ, 改善などによって均衡をはかっていた.
1950年代に入ってORが生産の様々な問題に適用され始めると, 組立作業を対象としたラインバランスの問題に組合せ最適化の観点から関心が示されるようになり, "組立ラインのバランシング (assembly line balancing)"と呼ばれ, 数理的な解析が試みられた. やがて多品種少量生産時代の訪れとともに, 混合品種組立ラインや品種切替組立ラインが一般化し, それらを対象とした問題である"混合品種組立ラインのバランシング"や"品種切替組立ラインのバランシング"が取り上げられて研究されるようになった. 同時に混合品種組立ラインに流す品種の順序づけ問題である"混合品種の順序づけ"が注目され, 特に自動車産業においては実務上の必要からその解法が各企業で考案され, 利用されるようになった.
また, 組立ての自動化につれて, 組立用ロボットを多用した組立ラインのための最適設計を意図したラインバランシングのモデルが研究されたり, プリント基板組立ラインのインサートマシンへの作業配分や順序づけを行うシステムが開発されている. 近年には, 半導体のウェファ製造職場を対象としたライン設計と運用の方式であるセルラインシステムがラインバランシングの考え方に基づいて開発されつつある.
2. ラインバランシングのモデル
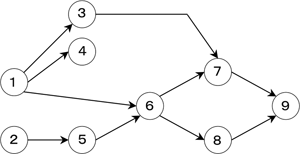
ラインバランシングの最初の精密なモデルは単一品種組立ラインを対象として構築された. これは1個の製品の組立てに必要な作業を合理性を失わない程度に分割して求めた 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle m\, } 個の作業要素を定義することが基本になっている. 次に潜在的な組立順序を示す作業要素間の先行関係を与える (図1参照).
図1:先行順位図 |
この二つの手続きを経て, ラインバランシング問題は以下に述べる制約の下で 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle m\, } 個の作業要素を 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle n\, } 個のワークステーションに配分する問題として定式化できる. ただし, ワークステーション数 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle n\, } は配分の結果として求められるものであり, 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle n\, } が最小になる配分を望ましいと考える.
制約(1) 作業要素の先行関係と作業要素が割り付けられるワークステーションの前後関係が矛盾しない.
制約(2) それぞれのワークステーションに割り付けられた作業要素の実施に要する標準時間である要素時間の合計が, 指定された時間であるサイクル時間 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle c\, } を超過しない.
制約(3) ある作業要素を特定のワークステーションに割り付ける "固定設備の制約", 2つ以上の作業要素を同一のワークステーションに割り付ける"グループ化の制約" など生産ライン特有の様々な付加的制約を満たす.
いま, 作業要素 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle i\, }
の要素時間を 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle e_i\, }
, ワークステーション 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle k\, }
に割り付けられた作業要素の集合を 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle S(k)\, }
, サイクル時間を 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle c\, }
で表すと, 制約(2)は次式によって示すことができる.
構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \sum_{i \in S(k)}{e_i} \le {c}, \ \ \ k = 1, 2, \ldots , n \, } 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle (1)\, }
(1)式の左辺を作業時間と呼び, 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle t_k\, }
で表す. また, サイクル時間と作業時間の差を遊び時間と呼び, 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle d_k\, }
で表すと, それらの関係は次式によって示される.
構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle d_k = c - t_k, \ \ \ k = 1, 2, \ldots , n \, } 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle (2)\, }
ラインバランシングにおいては, 通常, 作業時間の加法性が仮定され, 1個の製品の組立に要する総作業時間 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle T_w\, }
は次式で与えられると考える.
構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle T_w = \sum_{i = 1}^m e_i \, } 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle (3)\, }
目的関数はワークステーション数の最小化に等しく, これは組立ラインで生じる遊び時間の最小化として表すことができ, 次の評価尺度が用いられる.
構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle BD = \frac{\sum_{k = 1}^n {(c - t_k)}}{nc} \times 100 = \frac{nc - T_w}{nc} \times 100 \, } 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle (4)\, }
これはバランスロスと呼ばれ, 次に示す編成効率 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle E\, }
の最大化に等しい.
構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle E = \frac{T_w}{nc} \times 100 \, } 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle (5)\, }
3. 混合品種組立てへの拡張
前述のラインバランシングの方法を混合品種組立ラインに適用する効率の良い方法は, 対象にするすべての品種を同時に考慮するもので, そのためには統合先行順位図を用いる必要がある. これは, 品種別の先行順位図に含まれる品種間で共通の作業要素を各先行順位図が共有するように描いて作られる.
さらに, 混合品種組立の場合は各品種の生産量を考慮する必要があるので, ラインバランシングを計画期間における各ワークステーションの作業負荷を均等化する問題に置き換える. いま, 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle N\, } 品種の製品をある計画期間中に 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle f_j(j=1,2,\ldots ,N)\, } 個生産するものとする. 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle N\, } 品種の組立に必要な作業要素の総数を 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle m\, } , それぞれの要素時間を 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle e_i\, } で表す. 作業要素 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle i\, } と品種 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle j\, } の関係をクロネッカーのデルタ で示し, 作業要素 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle i\, } が品種 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle j\, } の組立に必要な場合は1, 不要な場合は0をとるように定めておく.
作業要素 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle i\, } が割り付けられたとき, そのワークステーションには計画期間 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle T\, } 中に次式で与えられる作業負荷がかかる.
構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle L_i = \sum_{j=1}^{N}f_j\delta_{ij}e_i, \ \ \ i = 1, 2, \ldots , m \, } 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle (6)\, }
したがって, 混合品種組立ての場合, (1)式に替えて次式により作業負荷の均衡をはかる.
構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \sum_{i \in S(k)}L_i \le T, \ \ \ k = 1, 2, \ldots , n \, } 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle (7)\, }
また, 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle T = c \sum_j f_j \, }
であるから編成効率は次式によって表わせる.
構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle E = \frac{\sum_i L_i}{nc \sum_j f_j} \times 100 = \frac{\sum_i L_i}{nT} \times 100 \, } 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle (8)\, }
参考文献
[1] 黒田 充, 『ラインバランシングとその応用』, 日刊工業新聞社, 1984.
[2] T.O. Prenting and N.C. Thomopoulos, Humanism and Technology in Assembly Line Systems, Spartan Books, 1974.