「《モダンポートフォリオ理論(概論)》」の版間の差分
| 3行目: | 3行目: | ||
金融資産をどのように組合せて自己に最も望ましいポートフォリオを選択するかの投資手法についての理論をポートフォリオ理論という. リスクを明示的に取扱うことを定量的に導入したマーコビィツ(H.M.Markowitz)以降の投資理論をそれ以前と区別してモダンポートフォリオ理論と呼んでいる. | 金融資産をどのように組合せて自己に最も望ましいポートフォリオを選択するかの投資手法についての理論をポートフォリオ理論という. リスクを明示的に取扱うことを定量的に導入したマーコビィツ(H.M.Markowitz)以降の投資理論をそれ以前と区別してモダンポートフォリオ理論と呼んでいる. | ||
| − | ポートフォリオ理論を平均分散モデルから説明しよう. ます資産$<math>i(i=1,2,...,n)\, </math>$への投資比率を$<math>x_{i}\, </math>$とする. $<math>x_{i} < 0\, </math>$は空売り(Short Sales)を表す. $<math>x_{i}\, </math>$を第$<math>i\, </math>$成分とするベクトル$<math>x=(x_{1},x_{2},\dots ,x_{n})^{\top}\, </math>$をポートフォリオと呼び, 制約条件 $<math>\sum_{i=1}^{n}x_i=1\, </math>$ を満足しなければならない. ここで$<math>\top\, </math>$ はベクトルの転置を表す. 資産$<math>i\, </math>$ の期待収益率を$<math>\mu_{i}\, </math>$, $<math>\mu=(\mu_1, \mu_2, \cdots, \mu_n)^{\top}\, </math>$, 資産$<math>i\, </math>$ での分散を$<math>\sigma_{i}^{2}\, </math>$, 資産$<math>i\, </math>$と$<math>j\, </math>$の共分散を$<math>\sigma_{ij}\, </math>$とする. このとき, ポートフォリオの期待収益率は$<math>\mu_p =\sum_{i=1}^n \mu_i x_i\, </math>$となり, ポートフォリオ収益率の分散は$<math>\sigma_{p}^{2} = \sum_{i=1}^{n}x_{j}^{2}\sigma_{i}^{2} +\sum_{i \not= j}x_{i}x_{j}\sigma_{ij}\, </math>$ となる. ベクトルと行列の記号を用いれば, ポートフォリオの期待収益率は$<math>\mu_{p} = x^{\top}\mu\, </math>$, 収益率の分散は$<math>\sigma_{p}^{2} = x^{\top}Vx\, </math>$ となる. $<math>V\, </math>$ は分散共分散行列で, 正定値行列である. すべての要素が1である$<math>n\, </math>$次元ベクトルを | + | ポートフォリオ理論を平均分散モデルから説明しよう. ます資産$<math>i(i=1,2,...,n)\, </math>$への投資比率を$<math>x_{i}\, </math>$とする. $<math>x_{i} < 0\, </math>$は空売り(Short Sales)を表す. $<math>x_{i}\, </math>$を第$<math>i\, </math>$成分とするベクトル$<math>x=(x_{1},x_{2},\dots ,x_{n})^{\top}\, </math>$をポートフォリオと呼び, 制約条件 $<math>\textstyle \sum_{i=1}^{n}x_i=1\, </math>$ を満足しなければならない. ここで$<math>\top\, </math>$ はベクトルの転置を表す. 資産$<math>i\, </math>$ の期待収益率を$<math>\mu_{i}\, </math>$, $<math>\mu=(\mu_1, \mu_2, \cdots, \mu_n)^{\top}\, </math>$, 資産$<math>i\, </math>$ での分散を$<math>\sigma_{i}^{2}\, </math>$, 資産$<math>i\, </math>$と$<math>j\, </math>$の共分散を$<math>\sigma_{ij}\, </math>$とする. このとき, ポートフォリオの期待収益率は$<math>\textstyle \mu_p =\sum_{i=1}^n \mu_i x_i\, </math>$となり, ポートフォリオ収益率の分散は$<math>\textstyle \sigma_{p}^{2} = \sum_{i=1}^{n}x_{j}^{2}\sigma_{i}^{2} +\sum_{i \not= j}x_{i}x_{j}\sigma_{ij}\, </math>$ となる. ベクトルと行列の記号を用いれば, ポートフォリオの期待収益率は$<math>\mu_{p} = x^{\top}\mu\, </math>$, 収益率の分散は$<math>\sigma_{p}^{2} = x^{\top}Vx\, </math>$ となる. $<math>V\, </math>$ は分散共分散行列で, 正定値行列である. すべての要素が1である$<math>n\, </math>$次元ベクトルを<math>{\mathbf 1}\, </math>とすれば, ポートフォリオの制約条件は$<math>x^{\top}{\mathbf 1} =1\, </math>$ となる. 投資のリターンをポートフォリオの期待収益率で測定し, 投資のリスクをその収益率の分散で代替する投資家を想定する. このような投資家は, さまざまな期待収益率$<math>\mu_{p}\, </math>$ の下で最小の分散を与えるポートフォリオを選択する. この投資家のポートフォリオ$<math>x\, </math>$ の選択問題を定式化すれば次の最小化問題となる. |
| − | <math>\begin{ | + | :<math>\begin{array}{rl} |
| − | \mbox{min.} \frac{1}{2}x^{\top}Vx | + | \mbox{min.} \frac{1}{2}x^{\top}Vx & \quad \quad (1)\\ |
| − | \ | + | \\ |
| − | \ | + | {\rm s.t. } \quad x^{\top}\mu = \mu_{p} & \quad \quad (2)\\ |
| − | + | \\ | |
| − | \ | + | x^{\top}{\mathbf 1} = 1 & \quad \quad (3) |
| − | \ | + | \end{array}\, </math> |
| − | \ | ||
| − | \end{ | ||
| 20行目: | 18行目: | ||
| − | <math>\frac{\partial L}{\partial x} = Vx - \lambda_{1}\mu - \lambda_{2}{\ | + | :<math>\begin{array}{c}\frac{\partial L}{\partial x} = Vx - \lambda_{1}\mu - \lambda_{2}{\mathbf 1} |
| − | = {\ | + | = {\mathbf 0}\\ |
| − | + | \\ | |
| − | + | \frac{\partial L}{\partial \lambda_{1}} = \mu_{p} - x^{\top}\mu = 0\\ | |
| − | \frac{\partial L}{\partial \lambda_{1}} = \mu_{p} - x^{\top}\mu = 0 | + | \\ |
| − | + | \frac{\partial L}{\partial \lambda_{2}} = 1 - x^{\top}{\mathbf 1} = 0 | |
| − | + | \end{array}\, </math> | |
| − | \frac{\partial L}{\partial \lambda_{2}} = 1 - x^{\top}{\ | ||
| 33行目: | 30行目: | ||
| − | <math> | + | <table> |
| − | x^{*} | + | <tr> |
| − | + | <td><math>x^{*} \, </math></td> | |
| + | <td><math>\; = \; V^{-1}(\lambda_{1}\mu + \lambda_{2}{\mathbf 1}) \, </math> </td> | ||
| + | </tr> | ||
| + | <tr> | ||
| + | <td></td> | ||
| + | <td><math>\; = \; V^{-1}(\mu,{\mathbf 1})\left[ \begin{array}{cc} | ||
{\lambda_{1}} \\ {\lambda_{2}} | {\lambda_{1}} \\ {\lambda_{2}} | ||
| − | \end{array} \right] \ | + | \end{array} \right] \, </math></td> |
| − | + | </tr> | |
| + | <tr> | ||
| + | <td></td> | ||
| + | <td><math>\; = \; V^{-1}(\mu,{\mathbf 1})A^{-1}\left[ \begin{array}{cc} | ||
{\mu_{p}} \\ {1} | {\mu_{p}} \\ {1} | ||
| − | \end{array} \right] | + | \end{array} \right] \quad \quad (4)\, </math></td> |
| − | \ | + | </tr> |
| + | </table> | ||
| 47行目: | 53行目: | ||
| − | <math> | + | :<math> |
A \equiv \left( \begin{array}{cc} | A \equiv \left( \begin{array}{cc} | ||
| − | \mu^{\top}V^{-1}\mu & \mu^{\top}V^{-1}{\ | + | \mu^{\top}V^{-1}\mu & \mu^{\top}V^{-1}{\mathbf 1} \\ |
| − | \mu^{\top}V^{-1}{\ | + | \mu^{\top}V^{-1}{\mathbf 1} & {\mathbf 1}^{\top}V^{-1}{\mathbf 1} |
\end{array} | \end{array} | ||
\right) | \right) | ||
| 57行目: | 63行目: | ||
b & c | b & c | ||
\end{array} | \end{array} | ||
| − | \right) | + | \right) \quad \quad (5) |
| − | + | \, </math> | |
| + | |||
| 64行目: | 71行目: | ||
| − | <math>\sigma_{p}^{2} = (\mu_{p},{\ | + | :<math> |
| + | \sigma_{p}^{2} = (\mu_{p},{\mathbf 1})A^{-1}(\mu,1)^{\top}V^{-1}VV^{-1}(\mu,{\mathbf | ||
1}) | 1}) | ||
A^{-1}\left[ \begin{array}{cc} | A^{-1}\left[ \begin{array}{cc} | ||
{\mu_{p}}\\{1} | {\mu_{p}}\\{1} | ||
| − | \end{array} \right] | + | \end{array} \right]\, </math> |
| − | + | :<math>= \frac{a-2b\mu_{p}+c\mu_{p}^{2}}{ac-b^{2}} | |
| − | = \frac{a-2b\mu_{p}+c\mu_{p}^{2}}{ac-b^{2}} | + | \, </math> <math> \quad \quad (6) \,</math> |
| − | \ | ||
| 78行目: | 85行目: | ||
| − | <math> | + | :<math> |
\frac{\sigma_{p}^{2}}{1/c} - \frac{(\mu_{p}-b/c)^{2}}{d/c^{2}} = 1 | \frac{\sigma_{p}^{2}}{1/c} - \frac{(\mu_{p}-b/c)^{2}}{d/c^{2}} = 1 | ||
| − | \ | + | \quad \quad (7) \,</math> |
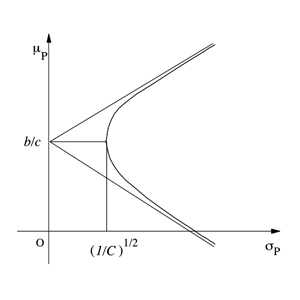
| − | を得る. (7)式を$<math>(\sigma_{p},\mu_{p})\, </math>$ 平面上に描けば, 図1の漸近線$<math>\mu_{p} = b/c \pm \sqrt{d/c} \ | + | を得る. (7)式を$<math>(\sigma_{p},\mu_{p})\, </math>$ 平面上に描けば, 図1の漸近線$<math>\mu_{p} = b/c \pm \sqrt{d/c} \; \sigma_{p}\, </math>$ をもつ双曲線である. |
| − | 0184-sawaki1. | + | <center><table><tr><td align=center>[[画像:0184-sawaki1-ff.png|center|図1:(σp, μp)平面上での効率的フロンティア]]</td></tr> |
| + | <td align=center>図1:<math>(\sigma_p , \mu_p) \, </math>平面上での効率的フロンティア</td></table></center> | ||
| − | |||
| − | |||
図1の双曲線に対応するポートフォリオをフロンティアポートフォリオと呼び, $<math>\mu_{p} = b/c\, </math>$ のとき最小の分散(すなわち標準偏差) を達成するポートフォリオを最小分散ポートフォリオという. この最小分散ポートフォリオの上側に位置するフロンティアポートフォリオを効率的ポートフォリオ (efficient portfolio) と呼ぶ. | 図1の双曲線に対応するポートフォリオをフロンティアポートフォリオと呼び, $<math>\mu_{p} = b/c\, </math>$ のとき最小の分散(すなわち標準偏差) を達成するポートフォリオを最小分散ポートフォリオという. この最小分散ポートフォリオの上側に位置するフロンティアポートフォリオを効率的ポートフォリオ (efficient portfolio) と呼ぶ. | ||
| − | 投資対象である前述の資産(危険資産)に無危険資産$<math>i=0\, </math>$ を追加し, その収益率(確定値) を $<math>\gamma_{0}\, </math>$ とする. ポートフォリオの制約条件 $<math>\sum_{i=0}^{n}x_i= 1\, </math>$ は, $<math>x_{0} = 1 - \sum_{i=1}^{n}x_{i}\, </math>$ を代入することによって除去され, ポートフォリオの様々な期待収益率<math>$\mu_{p}$の下で分散$\sigma_{p}^{2}\, </math>$を最小にする二次計画問題は | + | 投資対象である前述の資産(危険資産)に無危険資産$<math>i=0\, </math>$ を追加し, その収益率(確定値) を $<math>\gamma_{0}\, </math>$ とする. ポートフォリオの制約条件 $<math>\textstyle \sum_{i=0}^{n}x_i= 1\, </math>$ は, $<math>\textstyle x_{0} = 1 - \sum_{i=1}^{n}x_{i}\, </math>$ を代入することによって除去され, ポートフォリオの様々な期待収益率<math>$\mu_{p}$</math>の下で分散$<math>\textstyle \sigma_{p}^{2}\, </math>$を最小にする二次計画問題は |
| − | + | :<math>\begin{array}{ll} | |
| − | <math>\ | + | \mbox{min.} & \sigma_{p}^{2} = \frac{1}{2}x^{\top}Vx\\ |
| − | + | \\ | |
| − | + | {\rm s.t.}(\mu - \gamma_{0}{\mathbf 1})^{\top}x = \mu_{p} - | |
| − | + | \gamma_{0}\, | |
| − | \gamma_{0}\, </math> | + | \end{array}</math> |
| 107行目: | 113行目: | ||
| − | <math>\begin{ | + | :<math>\begin{array}{lll} |
| − | x^{*} = V^{-1}(\mu - \gamma_{0}{\ | + | x^{*} & = V^{-1}(\mu - \gamma_{0}{\mathbf 1})\frac{\mu_{p} - \gamma_{0}}{f}\quad \quad (8) \,</\\ |
| − | \ | + | \\ |
| + | x_{0}^{*} & = 1 - {\mathbf 1}^{\top}x^{*}\, </math> | ||
| − | <math>\ | + | となる. ここで$<math>f \equiv a - 2b\gamma_{0}+c \gamma_0^2\, </math>$である. このときの分散の最小値は |
| − | + | :<math>\sigma_{p}^{2} = x^{*\top}Vx^{*} = ( \mu_{p} - \gamma_{0})^2/f\, </math> | |
| − | |||
| − | |||
| − | <math>\sigma_{p}^{2} = x^{*\top}Vx^{*} = ( \mu_{p} - \gamma_{0})^2/f\, </math> | ||
となり, 書き換えれば | となり, 書き換えれば | ||
| − | + | <table> | |
| − | <math> | + | <tr> |
| − | \mu_{p} - \gamma_{0} = \left\{ \begin{array}{ | + | <td rowspan="2"><math>\mu_{p} - \gamma_{0} = \left\{ |
| − | + | \begin{array}{l} | |
| + | \\ | ||
| + | \\ | ||
| + | \\ | ||
\\ | \\ | ||
| − | + | \end{array} \right. </math></td> | |
| − | + | <td><math>\sqrt{f}\sigma_{p} ,&\mu_{p} \geq \gamma_{0} \,</math>のとき</td> | |
| − | \ | + | <td rowspan="2"><math>\quad \quad (8) </math> |
| + | </tr> | ||
| + | <tr> | ||
| + | <td><math>-\sqrt{f} \sigma_{p}, & \mu_{p} < \gamma_{0} \,</math>のとき</td> | ||
| + | </tr> | ||
| + | </table> | ||
| 136行目: | 148行目: | ||
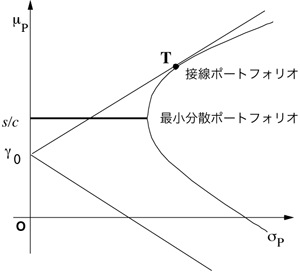
| − | 0184-sawaki2. | + | <center><table><tr><td align=center>[[画像:0184-sawaki2-ff.png|center|図2:n危険資産と無危険資産のポートフォリオ]]</td></tr> |
| + | <td align=center>図2: $<math>n\, </math>$危険資産と無危険資産のポートフォリオ</td></table></center> | ||
| + | |||
2007年7月13日 (金) 15:45時点における版
【もだんぽーとふぉりおりろん (がいろん) (modern portfolio theory)】
金融資産をどのように組合せて自己に最も望ましいポートフォリオを選択するかの投資手法についての理論をポートフォリオ理論という. リスクを明示的に取扱うことを定量的に導入したマーコビィツ(H.M.Markowitz)以降の投資理論をそれ以前と区別してモダンポートフォリオ理論と呼んでいる.
ポートフォリオ理論を平均分散モデルから説明しよう. ます資産$構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle i(i=1,2,...,n)\, } $への投資比率を$構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle x_{i}\, } $とする. $構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle x_{i} < 0\, } $は空売り(Short Sales)を表す. $構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle x_{i}\, } $を第$構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle i\, } $成分とするベクトル$構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle x=(x_{1},x_{2},\dots ,x_{n})^{\top}\, } $をポートフォリオと呼び, 制約条件 $構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \textstyle \sum_{i=1}^{n}x_i=1\, } $ を満足しなければならない. ここで$構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \top\, } $ はベクトルの転置を表す. 資産$構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle i\, } $ の期待収益率を$構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \mu_{i}\, } $, $構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \mu=(\mu_1, \mu_2, \cdots, \mu_n)^{\top}\, } $, 資産$構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle i\, } $ での分散を$構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \sigma_{i}^{2}\, } $, 資産$構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle i\, } $と$構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle j\, } $の共分散を$構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \sigma_{ij}\, } $とする. このとき, ポートフォリオの期待収益率は$構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \textstyle \mu_p =\sum_{i=1}^n \mu_i x_i\, } $となり, ポートフォリオ収益率の分散は$構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \textstyle \sigma_{p}^{2} = \sum_{i=1}^{n}x_{j}^{2}\sigma_{i}^{2} +\sum_{i \not= j}x_{i}x_{j}\sigma_{ij}\, } $ となる. ベクトルと行列の記号を用いれば, ポートフォリオの期待収益率は$構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \mu_{p} = x^{\top}\mu\, } $, 収益率の分散は$構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \sigma_{p}^{2} = x^{\top}Vx\, } $ となる. $構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle V\, } $ は分散共分散行列で, 正定値行列である. すべての要素が1である$構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle n\, } $次元ベクトルを構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle {\mathbf 1}\, } とすれば, ポートフォリオの制約条件は$構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle x^{\top}{\mathbf 1} =1\, } $ となる. 投資のリターンをポートフォリオの期待収益率で測定し, 投資のリスクをその収益率の分散で代替する投資家を想定する. このような投資家は, さまざまな期待収益率$構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \mu_{p}\, } $ の下で最小の分散を与えるポートフォリオを選択する. この投資家のポートフォリオ$構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle x\, } $ の選択問題を定式化すれば次の最小化問題となる.
- 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \begin{array}{rl} \mbox{min.} \frac{1}{2}x^{\top}Vx & \quad \quad (1)\\ \\ {\rm s.t. } \quad x^{\top}\mu = \mu_{p} & \quad \quad (2)\\ \\ x^{\top}{\mathbf 1} = 1 & \quad \quad (3) \end{array}\, }
行列$構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle V\, }
$ は正定値であるから上記の最小化問題は, 線形制約条件の下での凸二次計画問題となっているので, 一意の最適解をもつ. 乗数 $構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \lambda_{1}, \lambda_{2}\, }
$をもつラグランジュ関数$L$を導入すれば, 次の1階の条件は$構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle x\, }
$が最適解となるための必要かつ十分条件である.
- 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \begin{array}{c}\frac{\partial L}{\partial x} = Vx - \lambda_{1}\mu - \lambda_{2}{\mathbf 1} = {\mathbf 0}\\ \\ \frac{\partial L}{\partial \lambda_{1}} = \mu_{p} - x^{\top}\mu = 0\\ \\ \frac{\partial L}{\partial \lambda_{2}} = 1 - x^{\top}{\mathbf 1} = 0 \end{array}\, }
正定値行列$構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle V\, }
$ は逆行列をもつので, これらの式を連立して解けば, 最適解
| 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle x^{*} \, } | 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \; = \; V^{-1}(\lambda_{1}\mu + \lambda_{2}{\mathbf 1}) \, } |
| 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \; = \; V^{-1}(\mu,{\mathbf 1})\left[ \begin{array}{cc} {\lambda_{1}} \\ {\lambda_{2}} \end{array} \right] \, } | |
| 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \; = \; V^{-1}(\mu,{\mathbf 1})A^{-1}\left[ \begin{array}{cc} {\mu_{p}} \\ {1} \end{array} \right] \quad \quad (4)\, } |
を得る. ここで, 行列$構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle A\, }
$ は
- 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle A \equiv \left( \begin{array}{cc} \mu^{\top}V^{-1}\mu & \mu^{\top}V^{-1}{\mathbf 1} \\ \mu^{\top}V^{-1}{\mathbf 1} & {\mathbf 1}^{\top}V^{-1}{\mathbf 1} \end{array} \right) \equiv \left( \begin{array}{cc} a & b \\ b & c \end{array} \right) \quad \quad (5) \, }
で与えられる正定値行列で逆行列$構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle A^{-1}\, } $ をもつ. (詳しい導出は文献[1], [3]を参照)(4) 式はポートフォリオの期待収益率$構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \mu_{p}\, } $ が与えられたときの分散を最小にするポートフォリオであるから, (4)式を(1)式に代入すれば, 最小分散ポートフォリオの分散は
- 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \sigma_{p}^{2} = (\mu_{p},{\mathbf 1})A^{-1}(\mu,1)^{\top}V^{-1}VV^{-1}(\mu,{\mathbf 1}) A^{-1}\left[ \begin{array}{cc} {\mu_{p}}\\{1} \end{array} \right]\, }
- 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle = \frac{a-2b\mu_{p}+c\mu_{p}^{2}}{ac-b^{2}} \, } 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \quad \quad (6) \,}
となる. ここで, $構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle a,b,c\, }
$は(5) 式の行列$構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle A\, }
$ の各要素である. (6) 式を書き換えるために$構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle d=ac-b^{2}\, }
$とおけば,
- 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \frac{\sigma_{p}^{2}}{1/c} - \frac{(\mu_{p}-b/c)^{2}}{d/c^{2}} = 1 \quad \quad (7) \,}
を得る. (7)式を$構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle (\sigma_{p},\mu_{p})\, }
$ 平面上に描けば, 図1の漸近線$構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \mu_{p} = b/c \pm \sqrt{d/c} \; \sigma_{p}\, }
$ をもつ双曲線である.
| 図1:構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle (\sigma_p , \mu_p) \, } 平面上での効率的フロンティア |
図1の双曲線に対応するポートフォリオをフロンティアポートフォリオと呼び, $構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \mu_{p} = b/c\, } $ のとき最小の分散(すなわち標準偏差) を達成するポートフォリオを最小分散ポートフォリオという. この最小分散ポートフォリオの上側に位置するフロンティアポートフォリオを効率的ポートフォリオ (efficient portfolio) と呼ぶ.
投資対象である前述の資産(危険資産)に無危険資産$構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle i=0\, } $ を追加し, その収益率(確定値) を $構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \gamma_{0}\, } $ とする. ポートフォリオの制約条件 $構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \textstyle \sum_{i=0}^{n}x_i= 1\, } $ は, $構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \textstyle x_{0} = 1 - \sum_{i=1}^{n}x_{i}\, } $ を代入することによって除去され, ポートフォリオの様々な期待収益率構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle $\mu_{p}$} の下で分散$構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \textstyle \sigma_{p}^{2}\, } $を最小にする二次計画問題は
- 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \begin{array}{ll} \mbox{min.} & \sigma_{p}^{2} = \frac{1}{2}x^{\top}Vx\\ \\ {\rm s.t.}(\mu - \gamma_{0}{\mathbf 1})^{\top}x = \mu_{p} - \gamma_{0}\, \end{array}}
となる. このときの最適解は
- 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \begin{array}{lll} x^{*} & = V^{-1}(\mu - \gamma_{0}{\mathbf 1})\frac{\mu_{p} - \gamma_{0}}{f}\quad \quad (8) \,</\\ \\ x_{0}^{*} & = 1 - {\mathbf 1}^{\top}x^{*}\, }
となる. ここで$構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle f \equiv a - 2b\gamma_{0}+c \gamma_0^2\, }
$である. このときの分散の最小値は
- 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \sigma_{p}^{2} = x^{*\top}Vx^{*} = ( \mu_{p} - \gamma_{0})^2/f\, }
となり, 書き換えれば
| 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \mu_{p} - \gamma_{0} = \left\{ \begin{array}{l} \\ \\ \\ \\ \end{array} \right. } | 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \sqrt{f}\sigma_{p} ,&\mu_{p} \geq \gamma_{0} \,} のとき | 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \quad \quad (8) } |
| 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle -\sqrt{f} \sigma_{p}, & \mu_{p} < \gamma_{0} \,} のとき |
となる. もし $構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \gamma_{0} < a/c\, }
$ ならば, 危険資産のみからなるポートフォリオと (9) 式で与えられる無危険資産を含むポートフォリオとは図1の効率的フロンティアとが接するような接点ポートフォリオが存在して, 図2を得る.
| 図2: $構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle n\, } $危険資産と無危険資産のポートフォリオ |
図2: $構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle n\, } $危険資産と無危険資産のポートフォリオ}\label{c-g-01-zu2}
この接点ポートフォリオの下では, (9) 式より, 資産$構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle i\, }
$の超過収益率は
構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \begin{equation} \mu_{i} - \gamma_{0} = \beta_{i}(\mu_{p} - \gamma_{0}) \end{equation}\, }
と書ける. ただし$構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \beta_{i} = {\rm cov}(R_{i},R_{p})/{\rm var}(R_{p})\, }
$ である. ここで$構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle R_{i},R_{p}\, }
$は資産$構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle i\, }
$とポートフォリオ$構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle p\, }
$の収益率である. 市場のすべての投資家が資産の収益分布について同一の確率的信念を共有するならば, この平均分散モデルの下では全員の投資家は(8) 式で与えられる効率的ポートフォリオを保有することになり, この効率的ポートフォリオを市場ポートフォリオ(Market Portfolio) と呼び, その期待収益率を$構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \mu_{M}\, }
$, 標準偏差を$構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \sigma_{M}\, }
$とすれば, (10) 式は
構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \begin{equation} \mu_i - \gamma_{0} = \beta_{i}(\mu_{M} - \gamma_{0}) \end{equation}\, }
となる. ただし, $構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \beta_{i} = \sigma_{iM}/\sigma_{M}^{2}\, }
$である. この(11) 式をCAPM(資本資産評価モデル, Capital Asset Pricing Model)と呼び, 危険資産の平均超過収益率が満たすべき関係式である. $構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \beta_{i}\, }
$は危険資産$構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle i\, }
$のベータ値と呼ばれるもので, 市場ポートフォリオのリスクで測定した資産$i$のリスク尺度と見なされる.
CAPM は強い前提条件の下での平均分散モデルから導出された危険資産の平均超過収益率が満足すべき関係式であり, 実証研究をする上で理論的欠点を有している(Roll [5] を参照).
参考文献
[1] 澤木勝茂,『ファイナンスの数理』, 朝倉書店, 1994.
[2] 田畑吉雄,『数理ファイナンス論』, 牧野書店, 1993.
[3] H. L. Elton and N. J. Grunber, Modern Portfolio Theory and Investment Analysis, John Wiley & Sons, New York, 1991.
[4] H. Markowitz, Portfolio Selection, Wiley, New York, 1959.
[5] R. Roll, "A Critique of the Asset Pricing Theory's Tests," Journal of Financial Economics, 4 (1977), 129-176.