「利用者:Fujimoto/最短路問題」の版間の差分
(URL誤りを訂正) |
(数式修正(すべて画像に置換されるよう)) |
||
| 13行目: | 13行目: | ||
<!-- 原稿では影付きボックスですが、それはさすがに難しいので単なるquotationにしています --> | <!-- 原稿では影付きボックスですが、それはさすがに難しいので単なるquotationにしています --> | ||
<blockquote> | <blockquote> | ||
| − | ある有向グラフ<math>G = (V, E)</math> と各枝 <math>(v,w) \in E</math> に重み <math>l(v,w)</math> が付与されているネットワーク <math>N = (G,l)</math> が与えられているとする. このとき有向グラフ <math>G</math> の任意の 2 点 <math>s, t \in V</math> に対し, 点 <math>s</math> を始点とし, 点 <math>t</math> を終点とする有向パス <math>p</math> の中で, その長さ(パスに含まれる枝の重みの合計)が最小のパスを点 <math>s</math> から点 <math>t</math> への最短路 (shortest path) といい, 最短路を求める問題を最短路問題 (shortest path problem) という. | + | ある有向グラフ<math>G = (V, E)\, </math> と各枝 <math>(v,w) \in E\, </math> に重み <math>l(v,w)\, </math> が付与されているネットワーク <math>N = (G,l)\, </math> が与えられているとする. このとき有向グラフ <math>G\, </math> の任意の 2 点 <math>s, t \in V\, </math> に対し, 点 <math>s\, </math> を始点とし, 点 <math>t\, </math> を終点とする有向パス <math>p\, </math> の中で, その長さ(パスに含まれる枝の重みの合計)が最小のパスを点 <math>s\, </math> から点 <math>t\, </math> への最短路 (shortest path) といい, 最短路を求める問題を最短路問題 (shortest path problem) という. |
</blockquote> | </blockquote> | ||
| 28行目: | 28行目: | ||
==== ダイクストラ法 ==== | ==== ダイクストラ法 ==== | ||
| − | 1959年, E. W. Dijkstra<ref name="dijkstra">E. W. Dijkstra, "A Note on Two Problems in Connexion with Graphs," Numerische Mathematik, 1:269-271, 1959.</ref>によって提案された1対全最短路問題に対するアルゴリズムである. 探索するグラフ上の全ての枝の重みが非負でなければならないが, ベルマン・フォード法<ref>R. E. Bellman, "On a Routing Problem," Quarterly of Applied Mathematics, 16:87-90, 1958.</ref>に比べ効率的かつ高速である.ダイクストラ法は, ベルマン・フォード法と同じように動的計画法の一種とみなすことができるが, 点の探索の順序に特徴をもつ. 探索の途中で得られた始点 <math>s</math> からの距離の最小値をポテンシャルもしくは距離ラベルとよび, その値の小さい順に点の探索を行い,最短路および最短距離を確定していく. つまり, 各点に対し, <math>d(s) = 0, d(v) = +\infty (v \in V)</math> とするポテンシャル <math>d</math> を用意し, 探索点 <math>v</math> に接続する枝 <math>(v,w)</math> に対して, <math>d(v) + l(v,w) < d(w)</math> ならば <math>d(w) := l(v,w) + d(v)</math> とする操作を繰り返し行う. 終点 <math>t</math> が探索点になった時点で終了させることで, 1対1最短路問題も効率的に求解可能である. | + | 1959年, E. W. Dijkstra<ref name="dijkstra">E. W. Dijkstra, "A Note on Two Problems in Connexion with Graphs," Numerische Mathematik, 1:269-271, 1959.</ref>によって提案された1対全最短路問題に対するアルゴリズムである. 探索するグラフ上の全ての枝の重みが非負でなければならないが, ベルマン・フォード法<ref>R. E. Bellman, "On a Routing Problem," Quarterly of Applied Mathematics, 16:87-90, 1958.</ref>に比べ効率的かつ高速である.ダイクストラ法は, ベルマン・フォード法と同じように動的計画法の一種とみなすことができるが, 点の探索の順序に特徴をもつ. 探索の途中で得られた始点 <math>s\, </math> からの距離の最小値をポテンシャルもしくは距離ラベルとよび, その値の小さい順に点の探索を行い,最短路および最短距離を確定していく. つまり, 各点に対し, <math>d(s) = 0, d(v) = +\infty (v \in V)\, </math> とするポテンシャル <math>d\, </math> を用意し, 探索点 <math>v\, </math> に接続する枝 <math>(v,w)\, </math> に対して, <math>d(v) + l(v,w) < d(w)\, </math> ならば <math>d(w) := l(v,w) + d(v)\, </math> とする操作を繰り返し行う. 終点 <math>t\, </math> が探索点になった時点で終了させることで, 1対1最短路問題も効率的に求解可能である. |
===== ダイクストラ法のアルゴリズム ===== | ===== ダイクストラ法のアルゴリズム ===== | ||
| − | 1: ポテンシャル | + | 1: ポテンシャル <math>d\, </math>の初期設定 |
| − | 2: | + | 2: <math>S := V\, </math> |
3: '''while''' <math>S \neq \emptyset</math> '''do''' | 3: '''while''' <math>S \neq \emptyset</math> '''do''' | ||
| − | 4: <math>d(v)</math> が最小の点 <math>v \in S</math> を選択 | + | 4: <math>d(v)\, </math> が最小の点 <math>v \in S\, </math> を選択 |
| − | 5: | + | 5: <math>S := S \backslash \left\{ v \right\}\, </math> |
| − | 6: '''for all''' ( | + | 6: '''for all''' <math>(v, w)\, </math> '''do''' |
| − | 7: '''if''' <math>d(v) +l(v,w) < d(w)</math> '''then''' | + | 7: '''if''' <math>d(v) +l(v,w) < d(w)\, </math> '''then''' |
| − | 8: <math>d(w) := d(v) +l(v,w)</math> | + | 8: <math>d(w) := d(v) +l(v,w)\, </math> |
9: '''end if''' | 9: '''end if''' | ||
10: '''end for''' | 10: '''end for''' | ||
| 45行目: | 45行目: | ||
==== 高速化のための優先キューの利用 ==== | ==== 高速化のための優先キューの利用 ==== | ||
| − | ダイクストラ法は, 効率的かつ高速なアルゴリズムだが, 探索点を決定する操作([[#ダイクストラ法のアルゴリズム|アルゴリズム]]中の4行目,5行目)が, ボトルネックであることが知られている<ref name="dijkstra" />. 探索候補点集合(アルゴリズム中の | + | ダイクストラ法は, 効率的かつ高速なアルゴリズムだが, 探索点を決定する操作([[#ダイクストラ法のアルゴリズム|アルゴリズム]]中の4行目,5行目)が, ボトルネックであることが知られている<ref name="dijkstra" />. 探索候補点集合(アルゴリズム中の<math>S\, </math>)に対して優先キューを適用することで, 改善できる. |
==== 優先キューの実装方法 ==== | ==== 優先キューの実装方法 ==== | ||
優先キューとは, データを優先度によって操作するデータ構造のことである. ダイクストラ法に適用する優先キューは,<code>insert</code>, <code>decrease-key</code>, <code>extract-min</code>と呼ばれる操作に対応している必要がある. | 優先キューとは, データを優先度によって操作するデータ構造のことである. ダイクストラ法に適用する優先キューは,<code>insert</code>, <code>decrease-key</code>, <code>extract-min</code>と呼ばれる操作に対応している必要がある. | ||
| − | ;<code>insert</code>: ポテンシャル<math>d(v)</math>を優先度として, 点<math>v \in V</math>を優先キュー | + | ;<code>insert</code>: ポテンシャル<math>d(v)\, </math>を優先度として, 点<math>v \in V\, </math>を優先キュー<math>Q\, </math>へ挿入する. |
| − | ;<code>decrease-key</code>: 優先キュー内に格納されている点 <math>v \in Q</math>の優先度<math>d(v)</math>を, <math>d'(v)</math>に更新する. | + | ;<code>decrease-key</code>: 優先キュー内に格納されている点 <math>v \in Q\, </math>の優先度<math>d(v)\, </math>を, <math>d'(v)\, </math>に更新する. |
| − | ;<code>extract-min</code>: 優先度<math>d(v)</math>が最小である点<math>v \in Q</math>を取り出し, 点 | + | ;<code>extract-min</code>: 優先度<math>d(v)\, </math>が最小である点<math>v \in Q\, </math>を取り出し, 点<math>v\, </math>を次探索点とする. |
ダイクストラ法では, 繰り返しこれらの操作を行うことになるため, より効率的なものを適用することで, 高速化が可能になる. | ダイクストラ法では, 繰り返しこれらの操作を行うことになるため, より効率的なものを適用することで, 高速化が可能になる. | ||
| 58行目: | 58行目: | ||
===== 2-heap(バイナリ・ヒープ) ===== | ===== 2-heap(バイナリ・ヒープ) ===== | ||
| − | 2-heap<ref name="heap">J. Williams, "Heapsort," Communications of the ACM, 7:347-348, 1964.</ref>は, 図1のように, 親は高々2つの子を持つ木構造で構成される. 常に親の優先度は子より高い. 点数 | + | 2-heap<ref name="heap">J. Williams, "Heapsort," Communications of the ACM, 7:347-348, 1964.</ref>は, 図1のように, 親は高々2つの子を持つ木構造で構成される. 常に親の優先度は子より高い. 点数 <math>n\, </math>, 枝数 <math>m\, </math>に対して, 1対全最短路問題の計算量は <math>O((m+n)\log{n})\, </math> である. |
{| border="1" style="text-align:center; margin:0 auto" | {| border="1" style="text-align:center; margin:0 auto" | ||
| 77行目: | 77行目: | ||
===== Buckets(1 レベル・バケット)===== | ===== Buckets(1 レベル・バケット)===== | ||
| − | Buckets<ref name="dial">R. B. Dial, "Algorithm 360: Shortest Path Forest with Topological Ordering, " Comm. ACM, 12:632-633, 1969.</ref>は, 最大枝長 | + | Buckets<ref name="dial">R. B. Dial, "Algorithm 360: Shortest Path Forest with Topological Ordering, " Comm. ACM, 12:632-633, 1969.</ref>は, 最大枝長 <math>U\, </math>に対し, <math>U+1\, </math>個のバケットの循環リストとして構成される (図2). 点 <math>v\, </math>のポテンシャル<math>d(v)\, </math>に対し, <math>d(v)\mod(U+1)\, </math>により操作するバケットを決定する. 各バケット内のデータは双方向リストで結ばれており, 同一バケット内に格納されている点の優先度は常に等しい. 1対全最短路問題の計算量は, 点数<math>n\,</math>, 枝数<math>m\, </math>, 最大枝長<math>U\, </math>に対し, <math>O(m+nU)\, </math>である. |
#実行時間・メモリ要求量が, 最大枝長に依存する(重み小:高速, 重み大:低速). | #実行時間・メモリ要求量が, 最大枝長に依存する(重み小:高速, 重み大:低速). | ||
| 85行目: | 85行目: | ||
===== MLB(マルチレベル・バケット) ===== | ===== MLB(マルチレベル・バケット) ===== | ||
| − | MLB(Multi-Level Buckets)<ref name="mlb">A. V. Goldberg, "A Simple Shortest Path Algorithm with Linear Average Time," Technical Report STAR-TR-01-03, STAR Lab., InterTrust Tech., Inc., Santa Clara, CA, USA. 2001.</ref>は, ヒープ系優先キュー, バケット系優先キューの双方の有効な特性を融合させた優先キューである. グラフ特性の影響は小さく安定かつ高速であるが, 非常にメモリ要求量が大きい. 1レベル・バケットとは異なり,MLBではバケットは <math>\lceil \log{U} \rceil + 1</math>だけ用意すればよい. 点数 | + | MLB(Multi-Level Buckets)<ref name="mlb">A. V. Goldberg, "A Simple Shortest Path Algorithm with Linear Average Time," Technical Report STAR-TR-01-03, STAR Lab., InterTrust Tech., Inc., Santa Clara, CA, USA. 2001.</ref>は, ヒープ系優先キュー, バケット系優先キューの双方の有効な特性を融合させた優先キューである. グラフ特性の影響は小さく安定かつ高速であるが, 非常にメモリ要求量が大きい. 1レベル・バケットとは異なり,MLBではバケットは <math>\lceil \log{U} \rceil + 1\, </math>だけ用意すればよい. 点数 <math>n\, </math>, 枝数 <math>m\, </math>, 最大枝長 <math>U\, </math>に対し, 1対全最短路問題の計算量は<math>O(m + n\log{U})\, </math>となる. |
#グラフ特性の影響は小さく, 安定かつ高速 | #グラフ特性の影響は小さく, 安定かつ高速 | ||
| 92行目: | 92行目: | ||
=====優先キューの比較===== | =====優先キューの比較===== | ||
| − | 点数 | + | 点数 <math>n\, </math>, 枝数<math>m\, </math>, 最大枝数 <math>U\, </math>であるグラフに対して, 計算量をまとめると表1のようになる.1対全最短路問題では, 枝数分の<code>insert</code>と<code>decrease-key</code>, 点数分の<code>extract-min</code>を行うことになる.また, その特性は図3となる. これは, 比較的小さいグラフに対し, 各枝長を<math>2^{t} (t=[-10,-9,..,9,10])\, </math>倍し, 計算機実験を行った結果である. Buckets の特性がよく表れている. |
{| border="1" style="text-align:center" | {| border="1" style="text-align:center" | ||
| 99行目: | 99行目: | ||
|- | |- | ||
! 2-heap | ! 2-heap | ||
| − | | <math>O(\log{n})</math> || <math>O(\log{n})</math> || <math>O(\log{n}) </math> || <math>O((n+m)\log{n})</math> | + | | <math>O(\log{n})\, </math> || <math>O(\log{n})\, </math> || <math>O(\log{n}) \, </math> || <math>O((n+m)\log{n})\, </math> |
|- | |- | ||
! Buckets | ! Buckets | ||
| − | | <math>O(1)</math> || <math>O(1)</math> || <math>O(U)</math> || <math>O(m+nU)</math> | + | | <math>O(1)\, </math> || <math>O(1)\, </math> || <math>O(U)\, </math> || <math>O(m+nU)\, </math> |
|- | |- | ||
! MLB | ! MLB | ||
| − | | <math>O(1)</math> || <math>O(1)</math> || <math>O(\log{U})</math> || <math>O(m+n\log{U})</math> | + | | <math>O(1)\, </math> || <math>O(1)\, </math> || <math>O(\log{U})\, </math> || <math>O(m+n\log{U})\, </math> |
|} | |} | ||
2009年11月5日 (木) 16:51時点における最新版
【さいたんろもんだい (shortest path problem)】
概要
最短路問題は経路探索などの多くの応用を持ち, また他の最適化問題の子問題として用いられることも多く, 適用範囲の広い組合せ最適化問題である. そのため, 最短路問題を高速に解くことは重要な意味を持つ. 最短路問題に対する解法には, 安定的かつ効率的な高速なアルゴリズムが存在するが, 実問題は大規模(全米の道路ネットワークでは, 2400万点, 5800万枝にも及ぶ)になるため高速化が不可欠である.本解説では最短路問題の定義・種類を述べた後, 著名なアルゴリズムであるダイクストラ法に対する高速実装と実験結果[1]等について説明を行う.
詳説
最短路問題の定義と種類
最短路問題は次のような問題である.
ある有向グラフ構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle G = (V, E)\, } と各枝 に重み 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle l(v,w)\, } が付与されているネットワーク 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle N = (G,l)\, } が与えられているとする. このとき有向グラフ 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle G\, } の任意の 2 点 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle s, t \in V\, } に対し, 点 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle s\, } を始点とし, 点 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle t\, } を終点とする有向パス 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle p\, } の中で, その長さ(パスに含まれる枝の重みの合計)が最小のパスを点 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle s\, } から点 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle t\, } への最短路 (shortest path) といい, 最短路を求める問題を最短路問題 (shortest path problem) という.
最短路問題は次のように 3 種類に分けることができる.
- 1対全(single-source)最短路問題
- 1点から全点に対する最短路と最短距離(最短路の長さ)を求める問題. 非負の枝の重みを持つグラフ上ではダイクストラ(Dijkstra)法が, 負の重みを持つ枝がある場合にはベルマン・フォード(Bellman-Ford)法が有名である.
- 全対全(all-pairs)最短路問題
- 全点間の最短路と最短距離を求める問題. ワーシャル・フロイド(Warshall-Folyd)法が有名であるが, 1対全最短路問題アルゴリズムを各点に対して適用することでも求めることができる.
- 1対1(point-to-point)最短路問題
- 2点間の最短路と最短距離を求める問題.
探索アルゴリズムと実装方法
最短路問題に関する探索アルゴリズムの中でも, 最も頻繁に利用されるダイクストラ法を取り上げ, アルゴリズムの説明から, 高速化のための優先キューの適用方法・実装方法について示していく.
ダイクストラ法
1959年, E. W. Dijkstra[2]によって提案された1対全最短路問題に対するアルゴリズムである. 探索するグラフ上の全ての枝の重みが非負でなければならないが, ベルマン・フォード法[3]に比べ効率的かつ高速である.ダイクストラ法は, ベルマン・フォード法と同じように動的計画法の一種とみなすことができるが, 点の探索の順序に特徴をもつ. 探索の途中で得られた始点 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle s\, } からの距離の最小値をポテンシャルもしくは距離ラベルとよび, その値の小さい順に点の探索を行い,最短路および最短距離を確定していく. つまり, 各点に対し, 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle d(s) = 0, d(v) = +\infty (v \in V)\, } とするポテンシャル 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle d\, } を用意し, 探索点 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle v\, } に接続する枝 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle (v,w)\, } に対して, 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle d(v) + l(v,w) < d(w)\, } ならば 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle d(w) := l(v,w) + d(v)\, } とする操作を繰り返し行う. 終点 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle t\, } が探索点になった時点で終了させることで, 1対1最短路問題も効率的に求解可能である.
ダイクストラ法のアルゴリズム
1: ポテンシャル 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle d\, }
の初期設定
2: 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle S := V\, }
3: while 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle S \neq \emptyset}
do
4: 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle d(v)\, }
が最小の点 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle v \in S\, }
を選択
5: 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle S := S \backslash \left\{ v \right\}\, }
6: for all 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle (v, w)\, }
do
7: if 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle d(v) +l(v,w) < d(w)\, }
then
8: 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle d(w) := d(v) +l(v,w)\, }
9: end if
10: end for
11: end while
高速化のための優先キューの利用
ダイクストラ法は, 効率的かつ高速なアルゴリズムだが, 探索点を決定する操作(アルゴリズム中の4行目,5行目)が, ボトルネックであることが知られている[2]. 探索候補点集合(アルゴリズム中の構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle S\, } )に対して優先キューを適用することで, 改善できる.
優先キューの実装方法
優先キューとは, データを優先度によって操作するデータ構造のことである. ダイクストラ法に適用する優先キューは,insert, decrease-key, extract-minと呼ばれる操作に対応している必要がある.
insert- ポテンシャル構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle d(v)\, } を優先度として, 点構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle v \in V\, } を優先キュー構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle Q\, } へ挿入する.
decrease-key- 優先キュー内に格納されている点 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle v \in Q\, } の優先度構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle d(v)\, } を, 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle d'(v)\, } に更新する.
extract-min- 優先度構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle d(v)\, } が最小である点構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle v \in Q\, } を取り出し, 点構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle v\, } を次探索点とする.
ダイクストラ法では, 繰り返しこれらの操作を行うことになるため, より効率的なものを適用することで, 高速化が可能になる.
データ構造の選択
優先キューは, 木構造による安定した実行が可能なヒープ系データ構造と, データをルールに従いバケットに格納するバケット系データ構造とに分類が可能である. ここでは, それぞれの最も基本的なデータ構造であるバイナリ・ヒープと1レベル・バケットに加え, 実験的に最も高速であるといわれているマルチレベル・バケットを取り上げ, 比較を行う.
2-heap(バイナリ・ヒープ)
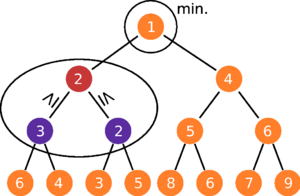
2-heap[4]は, 図1のように, 親は高々2つの子を持つ木構造で構成される. 常に親の優先度は子より高い. 点数 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle n\, } , 枝数 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle m\, } に対して, 1対全最短路問題の計算量は 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle O((m+n)\log{n})\, } である.
| Index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Data | 1 | 2 | 4 | 3 | 2 | 5 | 6 | 6 | 4 | 3 | 5 | 8 | 6 | 7 | 9 |
2-heapは以下の特徴をもつ.
- 木構造により実行性能が安定している.
- メモリ要求量が大変少なく, データの局所性を高めやすい.
- 木構造のためデータの読み書きが多発するので,データ交換操作がボトルネックとなりやすい.
Buckets(1 レベル・バケット)
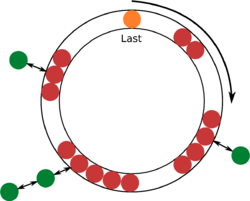
Buckets[5]は, 最大枝長 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle U\, } に対し, 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle U+1\, } 個のバケットの循環リストとして構成される (図2). 点 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle v\, } のポテンシャル構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle d(v)\, } に対し, 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle d(v)\mod(U+1)\, } により操作するバケットを決定する. 各バケット内のデータは双方向リストで結ばれており, 同一バケット内に格納されている点の優先度は常に等しい. 1対全最短路問題の計算量は, 点数構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle n\,} , 枝数構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle m\, } , 最大枝長構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle U\, } に対し, 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle O(m+nU)\, } である.
- 実行時間・メモリ要求量が, 最大枝長に依存する(重み小:高速, 重み大:低速).
- 道路ネットワークグラフと相性が良い.
MLB(マルチレベル・バケット)
MLB(Multi-Level Buckets)[6]は, ヒープ系優先キュー, バケット系優先キューの双方の有効な特性を融合させた優先キューである. グラフ特性の影響は小さく安定かつ高速であるが, 非常にメモリ要求量が大きい. 1レベル・バケットとは異なり,MLBではバケットは 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \lceil \log{U} \rceil + 1\, } だけ用意すればよい. 点数 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle n\, } , 枝数 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle m\, } , 最大枝長 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle U\, } に対し, 1対全最短路問題の計算量は構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle O(m + n\log{U})\, } となる.
- グラフ特性の影響は小さく, 安定かつ高速
- バケットを決定には高速なビット演算で行う
- メモリ要求量が非常に大きい
優先キューの比較
点数 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle n\, }
, 枝数構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle m\, }
, 最大枝数 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle U\, }
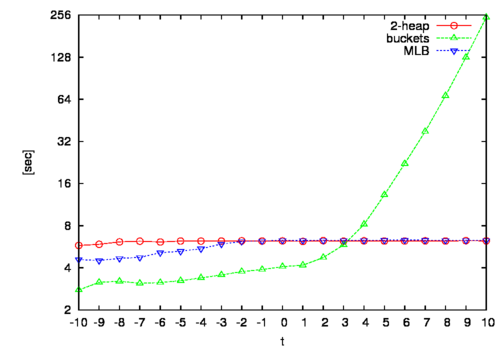
であるグラフに対して, 計算量をまとめると表1のようになる.1対全最短路問題では, 枝数分のinsertとdecrease-key, 点数分のextract-minを行うことになる.また, その特性は図3となる. これは, 比較的小さいグラフに対し, 各枝長を構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle 2^{t} (t=[-10,-9,..,9,10])\, }
倍し, 計算機実験を行った結果である. Buckets の特性がよく表れている.
insert |
decrease-key |
extract-min |
1対全最短路問題の計算量 | |
|---|---|---|---|---|
| 2-heap | 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle O(\log{n})\, } | 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle O(\log{n})\, } | 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle O(\log{n}) \, } | 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle O((n+m)\log{n})\, } |
| Buckets | 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle O(1)\, } | 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle O(1)\, } | 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle O(U)\, } | 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle O(m+nU)\, } |
| MLB | 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle O(1)\, } | 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle O(1)\, } | 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle O(\log{U})\, } | 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle O(m+n\log{U})\, } |
優先キューの性能
2-heap, Buckets, MLB それぞれの全米道路ネットワークに対しての計算機実験を行い, 実行時間とメモリ要求量をまとめると,表2, 表3のようになる. 用いたグラフデータは, 約 2400 万点, 約 5800 万枝にも及ぶ道路ネットワークを変換させた大規模な実データである(TIGER/Line[7]で公開されている). 実行時間は, ランダムに選択した1対1最短路問題を 256 回解いた際の平均である.
最短路問題では計算量に対してデータ量が大規模であるため, データ型によるメモリ使用量や実行時間に対する影響が大きい. 各変数が 32ビット整数型と 64ビット変数型の 2 種類の計算機実験の結果を記載する. グラフデータは大規模であるが, 32ビット整数型の範囲で収まるため, どちらの場合でもアルゴリズムは正しく終了するが, 距離ラベルはいずれも 64ビット整数である.
| 32ビット整数型 | 64ビット整数型 | |
|---|---|---|
| 2-heap | 2.47 | 3.14 |
| Buckets | 1.68 | 2.28 |
| MLB | 2.63 | 2.65 |
| 32ビット整数型 | 64ビット整数型 | |
|---|---|---|
| 2-heap | 1.27 | 1.99 |
| Buckets | 1.09 | 1.62 |
| MLB | 2.17 | 2.17 |
大規模最短路問題に対する高速処理システム
現在では Web 上で最短経路を求めるサービスが複数行われている(Google Maps[8]や最短路問題オンラインソルバー[9]など).
これらのシステムでは, 多くのユーザからの要求に対応する必要があるので, 単にダイクストラ法実行1回の処理を高速化するだけでなく, それらを並列に高速処理する技術が必要である.
ユーザからの要求量は時間帯や突発的な事象によって大きく変動するため, 最大需要を見越した計算資源を保有しておくのは無駄が多くコストも増大してしまう. そこでクラウド・コンピューティング技術を用いて, 高負荷時には自動的に計算機資源の増大を行うシステムなどが必要になってくる.
最近ではカーナビゲーション・システムの拡張として渋滞・事故情報をリアルタイムに把握しながら集約された大規模サーバで最短路を探索してユーザに結果を送信するシステムも構築されている. 動的な情報を考慮した最短路探索を行うことにより, これまでの経路探索に比べてより精度を向上させることができる. 特定の道路への集中を防ぐように交通量の分散を行うことで, 渋滞の緩和, 事故発生率の低下, 排出ガスの削減などを目指した交通管制を行うことも可能になると予想されている.
参考文献
- ↑ 安井雄一郎, 藤澤克樹, 笹島啓史, 後藤和茂, 宮本裕一郎, "大規模最短路問題に対するダイクストラ法の高速化," 2008 年度日本 OR 学会秋季研究発表会. 314-315, 2008.
- ↑ 2.0 2.1 E. W. Dijkstra, "A Note on Two Problems in Connexion with Graphs," Numerische Mathematik, 1:269-271, 1959.
- ↑ R. E. Bellman, "On a Routing Problem," Quarterly of Applied Mathematics, 16:87-90, 1958.
- ↑ J. Williams, "Heapsort," Communications of the ACM, 7:347-348, 1964.
- ↑ R. B. Dial, "Algorithm 360: Shortest Path Forest with Topological Ordering, " Comm. ACM, 12:632-633, 1969.
- ↑ A. V. Goldberg, "A Simple Shortest Path Algorithm with Linear Average Time," Technical Report STAR-TR-01-03, STAR Lab., InterTrust Tech., Inc., Santa Clara, CA, USA. 2001.
- ↑ http://www.census.gov/geo/www/tiger/tigerua/ua_tgr2k.html
- ↑ http://maps.google.com/
- ↑ http://opt.indsys.chuo-u.ac.jp/portal/