「経済発注量モデル」の版間の差分
(新しいページ: ''''【けいざいはっちゅうりょうもでる (economic order quantity model)】''' :参照:経済発注量公式') |
Sakasegawa (トーク | 投稿記録) |
||
| (2人の利用者による、間の2版が非表示) | |||
| 1行目: | 1行目: | ||
'''【けいざいはっちゅうりょうもでる (economic order quantity model)】''' | '''【けいざいはっちゅうりょうもでる (economic order quantity model)】''' | ||
| + | === 概要 === | ||
| − | : | + | |
| + | 在庫管理における定量発注方式での発注量決定のための公式でEOQと略称する. 単位時間あたりの需要 <math>D \,</math>(一定), 毎回の発注量 <math>Q \,</math>, 発注毎にかかる発注費用 <math>K \,</math>, 単位時間あたりの製品1個当りの在庫保持費用 <math>h \,</math>とし, 製品は即納を仮定する. 無限期間を想定して単位時間あたりの発注費用と在庫保持費用の総和を最小にする発注量 <math>Q^{*} \,</math>を求めると<math>Q^{*} = \sqrt{2KD/h} \,</math>となる. | ||
| + | === 詳説 === | ||
| + | 一般に, まとめて大量の数の生産や発注を行うと, 発注費用や段取り費用, 輸送単価が安くなるという「大量効果」が期待できる. 一度にまとめて発注する量のことを「ロットサイズ」と呼び, これに起因する在庫をロットサイズ在庫と呼ぶ. しかしその一方で, ロットサイズを大きくすると平均在庫量が大きくなり, 在庫保管費用の増大をもたらす. このように, 発注費用(段取り費用)と在庫保管費用の間には, ロットサイズを介したトレードオフの関係がある. このトレードオフを最適化する, すなわち発注費用と在庫保管費用の和を最小にするようなロットサイズの決定方法として, [[経済発注量モデル|経済発注量モデル (EOQモデル)]](EOQ model; economicorder quantity model) [1] [2] がある. | ||
| + | |||
| + | |||
| + | |||
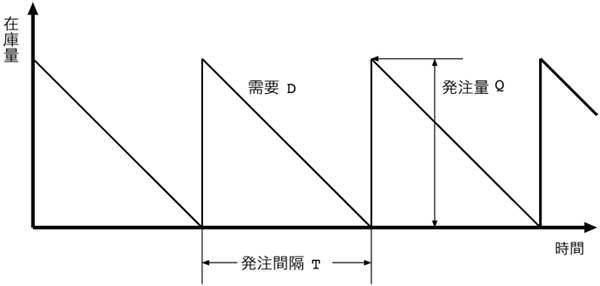
| + | <center><table><tr><td align=center>[[画像:0169-C-C-05+EOQ.png|center|図1:発注量と需要による在庫量の推移]]</td></tr> | ||
| + | <td align=center><br>図1:発注量と需要による在庫量の推移</td></table></center> | ||
| + | |||
| + | |||
| + | |||
| + | ここで, 単位時間あたりの需要が一定で, 在庫量が0になったら毎回同じ量の発注を行うような状況を考える. すなわち, 単位時間あたりの需要量を <math>D\, </math> , 発注間隔を <math>T\, </math> , 毎回の発注量を <math>Q\, </math> とし, 在庫は <math>D\, </math> の割合で連続的に減少するものとする (図1). また, 発注毎にかかる発注費用を <math>K\, </math> , 単位時間毎の製品1個あたりの在庫保管費用を <math>h\, </math> とし, 製品は発注と同時に到着する, すなわちリードタイムが0であるとする. | ||
| + | |||
| + | 初期在庫量が0でかつ無限期間を考える. 発注を行ってから在庫が0になるまでの総費用は, 平均在庫量が <math>Q/2\, </math> であることから, | ||
| + | |||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | K + \frac{hTQ}{2} | ||
| + | \, </math> | ||
| + | </center> | ||
| + | |||
| + | |||
| + | となる. 単位時間における費用 <math>f(Q)\, </math> は, これを <math>T\, </math> で除することによって | ||
| + | |||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | f(Q) = \frac{K}{T} + \frac{hQ}{2} | ||
| + | \, </math> | ||
| + | </center> | ||
| + | |||
| + | |||
| + | となるが, <math>Q=TD \, </math> なので, | ||
| + | |||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | f(Q) = \frac{KD}{Q} + \frac{hQ}{2} | ||
| + | \, </math> | ||
| + | </center> | ||
| + | |||
| + | |||
| + | となる. この <math>f(Q)\, </math> を <math>Q\, </math> で微分すれば, | ||
| + | |||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | f'(Q) = -\frac{KD}{Q^{2}} + \frac{h}{2} | ||
| + | \, </math> | ||
| + | </center> | ||
| + | |||
| + | |||
| + | となり, <math>f'(Q)=0\, </math> となる <math>Q\, </math> は, | ||
| + | |||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | Q^{*} = \sqrt{\frac{2KD}{h}} | ||
| + | \, </math> | ||
| + | </center> | ||
| + | |||
| + | |||
| + | で与えられ, <math>f(Q)\, </math> が凸関数なので, これが発注費用と在庫保管費用の総和 <math>f(Q)\, </math> を最小にする発注量である. また, そのときの費用総和は <math>f(Q^{*}) =\sqrt{2KDh} \, </math>, 最適発注間隔は <math>\displaystyle T^{*}=\sqrt{\frac{2K}{hD}} \, </math>となる. | ||
| + | |||
| + | このEOQモデルは基本的なモデルであるが, 実務的な観点から見れば, | ||
| + | |||
| + | :*需要の大きさが常に一定とは限らない | ||
| + | |||
| + | :*理論的に最適な発注間隔が分かっても, 実際にはそれを実行できるかどうか分からない | ||
| + | |||
| + | という問題点がある. | ||
| + | |||
| + | 前者に関しては, 有限期間で需要が変化するモデルとして扱う動的ロットサイズ決定問題がある. 後者に関しては, 例えば最適発注間隔が <math>\sqrt{5}\, </math> 日であることが分かったとしても, 通常の業務が週単位で行われていたりする現状を考えると, 実際に実行することは難しい. すなわち, 発注間隔 <math>T\, </math> が簡単に実現できるような値をとるような場合に限定して考えるのが自然である. | ||
| + | |||
| + | これに対して, 最小の発注間隔 <math>T_{L}\, </math> が存在し発注間隔 <math>T\, </math> は <math>T_{L}\, </math> の2のべき乗でなければならない, すなわち, | ||
| + | |||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | T=2^{k} T_{L},\ \ \ k\in \{0,1,2,3\ldots \} | ||
| + | \, </math> | ||
| + | </center> | ||
| + | |||
| + | |||
| + | と仮定する, [[2のべき乗方策]] [4] と呼ばれる方策がある. | ||
| + | |||
| + | ここで, 最初に述べたEOQモデルにおいて, 発注間隔 <math>T\, </math> の場合の単位時間あたりの平均費用を <math>\varphi(T)\, </math> , <math>g = \displaystyle{\frac{hD}{2}} \, </math> とすると, | ||
| + | |||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | \varphi(T) = \frac{KD}{Q} + \frac{hQ}{2} = \frac{K}{T} + gT | ||
| + | \, </math> | ||
| + | </center> | ||
| + | |||
| + | |||
| + | となり, | ||
| + | |||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | \varphi(2^{k+1} \cdot T_{L}) \geq \varphi(2^{k} \cdot T_{L}) | ||
| + | \, </math> | ||
| + | </center> | ||
| + | |||
| + | |||
| + | なる最小の非負の整数 <math>k\, </math> を見つけることに帰着し, | ||
| + | |||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | \frac{1}{\sqrt{2}}T^{*} \leq 2^k \cdot T_{L} \leq \sqrt{2} T^{*} | ||
| + | \, </math> | ||
| + | </center> | ||
| + | |||
| + | |||
| + | となることがわかる. すなわち, 上記の不等式を満足するように <math>k\, </math> を選ぶことによって, そのとき | ||
| + | |||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | \frac{\varphi(T)}{\varphi(T^{*})} \leq \frac{1}{2} \left( \sqrt{2} + \frac{1}{\sqrt{2}} \right) \approx 1.06 | ||
| + | \, </math> | ||
| + | </center> | ||
| + | |||
| + | |||
| + | となり, 最適な発注間隔の場合よりも最大約 6%の過剰コストで済む. | ||
| + | |||
| + | |||
| + | ---- | ||
| + | '''参考文献''' | ||
| + | |||
| + | [1] F. Harris, ''Operations and Costs,'' A. W. Shaw Co., 1915. | ||
| + | |||
| + | [2] R. H. Wilson, "A Scientific Routine for Stock Control," ''Harvard Business Review'', '''13'''(1934), 116-128 | ||
| + | |||
| + | [3] J. Bramel and D. Simchi-Levi, ''The Logic of Logistics'', Springer, 1997. | ||
| + | |||
| + | [4] J. A. Muckstadt and R. O. Roundy. "Analysis of Multistage Production Systems," in'' Logistics of Production and Inventory'', S. C. Graves, A. H. G. Rinnooy Kan and P. H. Zipkin, eds., North-Holland, 1993. | ||
| + | |||
| + | [[category:生産・在庫・ロジスティクス|けいざいはっちゅうりょうもでる]] | ||
2008年4月2日 (水) 16:04時点における最新版
【けいざいはっちゅうりょうもでる (economic order quantity model)】
概要
在庫管理における定量発注方式での発注量決定のための公式でEOQと略称する. 単位時間あたりの需要 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle D \,} (一定), 毎回の発注量 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle Q \,} , 発注毎にかかる発注費用 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle K \,} , 単位時間あたりの製品1個当りの在庫保持費用 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle h \,} とし, 製品は即納を仮定する. 無限期間を想定して単位時間あたりの発注費用と在庫保持費用の総和を最小にする発注量 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle Q^{*} \,} を求めると構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle Q^{*} = \sqrt{2KD/h} \,} となる.
詳説
一般に, まとめて大量の数の生産や発注を行うと, 発注費用や段取り費用, 輸送単価が安くなるという「大量効果」が期待できる. 一度にまとめて発注する量のことを「ロットサイズ」と呼び, これに起因する在庫をロットサイズ在庫と呼ぶ. しかしその一方で, ロットサイズを大きくすると平均在庫量が大きくなり, 在庫保管費用の増大をもたらす. このように, 発注費用(段取り費用)と在庫保管費用の間には, ロットサイズを介したトレードオフの関係がある. このトレードオフを最適化する, すなわち発注費用と在庫保管費用の和を最小にするようなロットサイズの決定方法として, 経済発注量モデル (EOQモデル)(EOQ model; economicorder quantity model) [1] [2] がある.
図1:発注量と需要による在庫量の推移 |
ここで, 単位時間あたりの需要が一定で, 在庫量が0になったら毎回同じ量の発注を行うような状況を考える. すなわち, 単位時間あたりの需要量を 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle D\, } , 発注間隔を 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle T\, } , 毎回の発注量を 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle Q\, } とし, 在庫は 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle D\, } の割合で連続的に減少するものとする (図1). また, 発注毎にかかる発注費用を 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle K\, } , 単位時間毎の製品1個あたりの在庫保管費用を 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle h\, } とし, 製品は発注と同時に到着する, すなわちリードタイムが0であるとする.
初期在庫量が0でかつ無限期間を考える. 発注を行ってから在庫が0になるまでの総費用は, 平均在庫量が 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle Q/2\, } であることから,
構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle K + \frac{hTQ}{2} \, }
となる. 単位時間における費用 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle f(Q)\, }
は, これを 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle T\, }
で除することによって
構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle f(Q) = \frac{K}{T} + \frac{hQ}{2} \, }
となるが, 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle Q=TD \, }
なので,
構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle f(Q) = \frac{KD}{Q} + \frac{hQ}{2} \, }
となる. この 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle f(Q)\, }
を 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle Q\, }
で微分すれば,
構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle f'(Q) = -\frac{KD}{Q^{2}} + \frac{h}{2} \, }
となり, 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle f'(Q)=0\, }
となる 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle Q\, }
は,
構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle Q^{*} = \sqrt{\frac{2KD}{h}} \, }
で与えられ, 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle f(Q)\, }
が凸関数なので, これが発注費用と在庫保管費用の総和 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle f(Q)\, }
を最小にする発注量である. また, そのときの費用総和は 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle f(Q^{*}) =\sqrt{2KDh} \, }
, 最適発注間隔は 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \displaystyle T^{*}=\sqrt{\frac{2K}{hD}} \, }
となる.
このEOQモデルは基本的なモデルであるが, 実務的な観点から見れば,
- 需要の大きさが常に一定とは限らない
- 理論的に最適な発注間隔が分かっても, 実際にはそれを実行できるかどうか分からない
という問題点がある.
前者に関しては, 有限期間で需要が変化するモデルとして扱う動的ロットサイズ決定問題がある. 後者に関しては, 例えば最適発注間隔が 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \sqrt{5}\, } 日であることが分かったとしても, 通常の業務が週単位で行われていたりする現状を考えると, 実際に実行することは難しい. すなわち, 発注間隔 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle T\, } が簡単に実現できるような値をとるような場合に限定して考えるのが自然である.
これに対して, 最小の発注間隔 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle T_{L}\, } が存在し発注間隔 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle T\, } は 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle T_{L}\, } の2のべき乗でなければならない, すなわち,
構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle T=2^{k} T_{L},\ \ \ k\in \{0,1,2,3\ldots \} \, }
と仮定する, 2のべき乗方策 [4] と呼ばれる方策がある.
ここで, 最初に述べたEOQモデルにおいて, 発注間隔 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle T\, } の場合の単位時間あたりの平均費用を 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \varphi(T)\, } , 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle g = \displaystyle{\frac{hD}{2}} \, } とすると,
構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \varphi(T) = \frac{KD}{Q} + \frac{hQ}{2} = \frac{K}{T} + gT \, }
となり,
構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \varphi(2^{k+1} \cdot T_{L}) \geq \varphi(2^{k} \cdot T_{L}) \, }
なる最小の非負の整数 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle k\, }
を見つけることに帰着し,
構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \frac{1}{\sqrt{2}}T^{*} \leq 2^k \cdot T_{L} \leq \sqrt{2} T^{*} \, }
となることがわかる. すなわち, 上記の不等式を満足するように 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle k\, }
を選ぶことによって, そのとき
構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://en.wikipedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \frac{\varphi(T)}{\varphi(T^{*})} \leq \frac{1}{2} \left( \sqrt{2} + \frac{1}{\sqrt{2}} \right) \approx 1.06 \, }
となり, 最適な発注間隔の場合よりも最大約 6%の過剰コストで済む.
参考文献
[1] F. Harris, Operations and Costs, A. W. Shaw Co., 1915.
[2] R. H. Wilson, "A Scientific Routine for Stock Control," Harvard Business Review, 13(1934), 116-128
[3] J. Bramel and D. Simchi-Levi, The Logic of Logistics, Springer, 1997.
[4] J. A. Muckstadt and R. O. Roundy. "Analysis of Multistage Production Systems," in Logistics of Production and Inventory, S. C. Graves, A. H. G. Rinnooy Kan and P. H. Zipkin, eds., North-Holland, 1993.