「《AHP》」の版間の差分

提供: ORWiki
ナビゲーションに移動 検索に移動
(新しいページ: ''''【えーえいちぴー (AHP (Analytic Hierarchy Process)) 】''' 　階層化意思決定法とも訳されるが, 通常AHPと呼ばれる. トマス・サーティ...')
 
 
(2人の利用者による、間の3版が非表示)
6行目: 6行目:
  
  
−
\begin{figure}[ht]
+
<center><table><tr><td align=center>[[画像:0224-a-h-01-kiso-zu1r.png|center|図１：階層図]]</td></tr>
−
% \psbox{ZU-A-H-01-01}
+
<td align=center><br>図１：階層図</td></table></center>
−
\begin{center}
 
−
%\psbox[scale=0.7]{A-H-01-kiso-zu1.eps}
 
−
\includegraphics[scale=0.6]{0224-a-h-01-kiso-zu1r.eps}
 
−
\end{center}
 
−
\caption{階層図}\label{A-H-01-01}
 
−
\end{figure}
 
  
  
−
　この階層図の上で, 最上層の問題から見た各代替案の重要度を求めて意思決定の支援をしたいのである. そのためにはまず第1層の問題から見た第2層の評価基準 $c_k$ の重要度 $u_k$ を求める. さらに各評価基準 $c_k$ の下の代替案 $a_j$ の(局所)重要度 $v_{kj}$ を求める. そのうえで, 代替案 $a_j$ ごとに, 各評価基準 $c_k$ の下での重要度 $v_{kj}$ の, 評価基準の重要度 $u_k$ で重み付けをした和 $\sum u_k v_{kj}$ を取って, 代替案 $a_j$ の(総合)重要度とする. この重要度を求める過程で一対比較評価をしている.  
+
　この階層図の上で, 最上層の問題から見た各代替案の重要度を求めて意思決定の支援をしたいのである. そのためにはまず第1層の問題から見た第2層の評価基準 <math>c_k\, </math> の重要度 <math>u_k\, </math> を求める. さらに各評価基準 <math>c_k\, </math> の下の代替案 <math>a_j\, </math> の(局所)重要度 <math>v_{kj}\, </math> を求める. そのうえで, 代替案 <math>a_j\, </math> ごとに, 各評価基準 <math>c_k\, </math> の下での重要度 <math>v_{kj}\, </math> の, 評価基準の重要度 <math>u_k\, </math> で重み付けをした和 <math>\textstyle \sum u_k v_{kj}\, </math> を取って, 代替案 <math>a_j\, </math> の(総合)重要度とする. この重要度を求める過程で一対比較評価をしている.  
  
−
　[一対比較から重要度の計算へ]: 例えば評価基準が4つあったらそれらを $c_1$ , $c_2$ , $c_3$ , $c_4$と表し, それぞれを要素と呼ぶ. 4要素あると $4(4-1)/2=6$ 組の対があるのでそれらの対の2要素の重要さを比較判断する(一対比較する). 要素 $i$ を要素 $j$ と比べて値 $a_{ij}$ を表1に従って定め, 行列に表したもの $A=[a_{ij}]$ を[[一対比較行列]]と呼ぶ.  
+
　[一対比較から重要度の計算へ]: 例えば評価基準が4つあったらそれらを <math>c_1\, </math>, <math>c_2\, </math>, <math>c_3\, </math>, <math>c_4\, </math>と表し, それぞれを要素と呼ぶ. 4要素あると <math>4(4-1)/2=6\, </math> 組の対があるのでそれらの対の2要素の重要さを比較判断する(一対比較する). 要素 <math>i\, </math> を要素 <math>j\, </math> と比べて値 <math>a_{ij}\, </math> を表1に従って定め, 行列に表したもの <math>A=[a_{ij}]\, </math> を[[一対比較行列]]と呼ぶ.  
  
  
−
\begin{table}
+
<center>
−
\begin{center}
+
<caption>表１：一対比較の基準尺度<br></caption>
−
\caption{一対比較の基準尺度}\label{A-H-01-02}
+
<table width="300">
−
\begin{tabular}{lcc}
+
<tr>
−
要素 $i$ が要素 $j$ に比べて & & $a_{ij}$ \\
+
<td colspan="2" align="left">要素 <math>i\, </math> が要素 <math>j\, </math> に比べて</td>
−
\hline
+
<td align="center" width="50"><math>a_{ij}\, </math></td>
−
同程度に重要なとき & $\rightarrow$ & $1$ \\
+
</tr>
−
やや重要           & $\rightarrow$ & $3$ \\
+
<tr>
−
かなり重要         & $\rightarrow$ & $5$ \\
+
<td colspan="3" align="left">
−
非常に重要         & $\rightarrow$ & $7$ \\
+
<hr>
−
圧倒的に重要       & $\rightarrow$ & $9$ \\
+
</td>
−
\hline
+
</tr>
−
\end{tabular}
+
<tr>
−
\end{center}
+
<td align="left">同程度に重要なとき</td>
−
\begin{center}
+
<td align="center" width="50"><math>\rightarrow\, </math></td>
−
\noindent 2, 4, 6, 8 という中間値も適宜使う. \\
+
<td align="center" width="50">1</td>
−
\noindent $a_{ji}=1/a_{ij}\; ,\; a_{ii}=1$ とする.  
+
</tr>
−
\end{center}
+
<tr>
−
\end{table}
+
<td align="left">やや重要 </td>
 +
<td align="center" width="50"><math>\rightarrow\, </math></td>
 +
<td align="center" width="50">3</td>
 +
</tr>
 +
<tr>
 +
<td align="left">かなり重要 </td>
 +
<td align="center" width="50"><math>\rightarrow\, </math></td>
 +
<td align="center" width="50">5</td>
 +
</tr>
 +
<tr>
 +
<td align="left">非常に重要 </td>
 +
<td align="center" width="50"><math>\rightarrow\, </math></td>
 +
<td align="center" width="50">7</td>
 +
</tr>
 +
<tr>
 +
<td align="left">圧倒的に重要</td>
 +
<td align="center" width="50"><math>\rightarrow\, </math></td>
 +
<td align="center" width="50">9</td>
 +
</tr>
 +
<tr>
 +
<td colspan="3" align="left">
 +
<hr>
 +
</td>
 +
</tr>
 +
<tr>
 +
<td colspan="3" align="center">2, 4, 6, 8 という中間値も適宜使う. </td>
 +
</tr>
 +
<tr>
 +
<td colspan="3" align="center"><math>a_{ji}=1/a_{ij}\; ,\; a_{ii}=1\, </math> とする. </td>
 +
</tr>
 +
</table></center>
  
−
　要素 $c_j$ の重要度(ウエイト (weight)あるいはプライオリティ (priority)とも呼ぶ)を $w_j$ とすると, $w_i / w_j$ を $a_{ij}$ で推定していると考えられる. 行列 $A$ の要素 $a_{ij}$ を $w_i / w_j$ で置き換えた上でベクトル $\mbox{\boldmath $w$}$ を右から掛けると,
 
  
 +
　要素 <math>c_j\, </math> の重要度(ウエイト (weight)あるいはプライオリティ (priority)とも呼ぶ)を <math>w_j\, </math> とすると, <math>w_i / w_j\, </math> を <math>a_{ij}\, </math> で推定していると考えられる. 行列 <math>A\, </math> の要素 <math>a_{ij}\, </math> を <math>w_i / w_j\, </math> で置き換えた上でベクトル <math>{\boldsymbol w}\, </math> を右から掛けると,
  
−
\begin{array}{ccl}
 
−
A \mbox{\boldmath $w$} & = & \left[ \begin{array}{cccc}
 
−
  1        & w_1 / w_2 & w_1 / w_3 & w_1 / w_4 \\
 
−
  w_2 / w_1 & 1        & w_2 / w_3 & w_2 / w_4 \\
 
−
  w_3 / w_1 & w_3 / w_2 & 1        & w_3 / w_4 \\
 
−
  w_4 / w_1 & w_4 / w_2 & w_4 / w_3 & 1
 
−
  \end{array} \right] \mbox{\boldmath $w$} \\
 
−
  & = & n[w_1 \dots w_4]^{\top}
 
−
\end{array}
 
  
 +
<table align="center">
 +
<tr>
 +
<td><math>A {\boldsymbol w}\, </math></td>
 +
<td><math>=\, </math></td>
 +
<td> <math>\left[ \begin{array}{cccc}<br>
 +
  1        & w_1 / w_2 & w_1 / w_3 & w_1 / w_4 \\
 +
  w_2 / w_1 & 1    & w_2 / w_3 & w_2 / w_4 \\
 +
  w_3 / w_1 & w_3 / w_2 & 1    & w_3 / w_4 \\
 +
  w_4 / w_1 & w_4 / w_2 & w_4 / w_3 & 1
 +
  \end{array} \right] {\boldsymbol w}\, </math></td>
 +
</tr>
 +
<tr>
 +
<td><br>
 +
</td>
 +
<td><math>=\, </math></td>
 +
<td><math>n [ w_1 \dots w_4 ] ^{\top}\, </math></td>
 +
</tr>
 +
</table>
  
−
で, これは固有方程式 $A \mbox{\boldmath $w$}=\lambda \mbox{\boldmath $w$}$ の形をしている. 行列 $A$ の階数は $1$ であり, $A$ の固有値は最大固有値が $n$ (要素数), その他のものは $0$ であることがいえるので, $A=[a_{ij}]$ の最大固有値 $\lambda_{\max}$に対する固有ベクトルを $\mbox{\boldmath $w$}$ の値とする. この際に $\mbox{\boldmath $w$}$ のすべての成分の和が $1$ であるほうが便利なので, $\mbox{\boldmath $w$}$ の成分を正規化した(各成分を$\sum w_j$で割った)ものを重要度とする.
 
  
−
　[整合性]: 人間は一対比較で次のように整合性に欠ける判断をすることがある. (a)要素 AとBを比べるとBが好ましく, BとCを比べるとCが好ましいのに, AとCを比べるとAが好ましいとする. (b)AはBに比べて4倍程度強い, Cに比べると5倍くらい強いと判断したのに, BはCの7倍強いとする. もし整合性が完全にあれば, 3つの要素 $i, j, k$ の間で$a_{ij} = a_{ik}a_{kj}$ が成り立つはずである. 実際に整合性が完全にあると一対比較行列の最大固有値が要素の数に一致する($\lambda_{\max}=n$)のでそのずれを$n$の大きさによらぬようにした $(\lambda_{\max}-n)/(n-1)$ を[[整合度 (AHP一対比較の)|整合度]]とする.この値が$0.1$を超えると整合性が欠けることが強いので, 判断を再検討するなりやり直す必要があるとされている.
+
で, これは固有方程式 <math>A {\boldsymbol w}=\lambda {\boldsymbol w}\, </math> の形をしている. 行列 <math>A\, </math> の階数は <math>1\, </math> であり, <math>A\, </math> の固有値は最大固有値が <math>n\, </math> (要素数), その他のものは <math>0\, </math> であることがいえるので, <math>A=[a_{ij}]\, </math> の最大固有値 <math>\lambda_{\max}\, </math>に対する固有ベクトルを <math>{\boldsymbol w}\, </math> の値とする. この際に <math>{\boldsymbol w}\, </math> のすべての成分の和が <math>1\, </math> であるほうが便利なので, <math>{\boldsymbol w}\, </math> の成分を正規化した(各成分を<math>\textstyle \sum w_j\, </math>で割った)ものを重要度とする.
  
−
　また, 一対比較の結果に使われる数値をランダムに配置した同じサイズの多数の行列の整合度の平均値(ランダム整合度)に対するこの整合度の比(整合比)も$0.1$以下が好ましいとされ, 整合性の判断に用いられている.  
+
　[整合性]: 人間は一対比較で次のように整合性に欠ける判断をすることがある. (a)要素 AとBを比べるとBが好ましく, BとCを比べるとCが好ましいのに, AとCを比べるとAが好ましいとする. (b)AはBに比べて4倍程度強い, Cに比べると5倍くらい強いと判断したのに, BはCの7倍強いとする. もし整合性が完全にあれば, 3つの要素 <math>i, j, k\, </math> の間で<math>a_{ij} = a_{ik}a_{kj}\, </math> が成り立つはずである. 実際に整合性が完全にあると一対比較行列の最大固有値が要素の数に一致する(<math>\lambda_{\max}=n\, </math>)のでそのずれを<math>n\, </math>の大きさによらぬようにした <math>(\lambda_{\max}-n)/(n-1)\, </math> を[[整合度 (AHP一対比較の)|整合度]]とする.この値が<math>0.1\, </math>を超えると整合性が欠けることが強いので, 判断を再検討するなりやり直す必要があるとされている.
 +
 
 +
　また, 一対比較の結果に使われる数値をランダムに配置した同じサイズの多数の行列の整合度の平均値(ランダム整合度)に対するこの整合度の比(整合比)も<math>0.1\, </math>以下が好ましいとされ, 整合性の判断に用いられている.  
  
 
　[ANPへ]: AHPでは階層図の各層の要素の間には従属性がないものとしている. しかし実際には, 層の中の要素の間どころか, 上下の層の要素の間にも従属性が強い場合もある. そこまで拡張すると問題のモデルは階層図ではなくネットワークになってくるので, その分野はANP(Analytic Network Process)と呼ばれている. 特に1990年前後からそのようなモデルの研究や応用が進んでいる[Saaty(1996), 高橋(1998)].  
 
　[ANPへ]: AHPでは階層図の各層の要素の間には従属性がないものとしている. しかし実際には, 層の中の要素の間どころか, 上下の層の要素の間にも従属性が強い場合もある. そこまで拡張すると問題のモデルは階層図ではなくネットワークになってくるので, その分野はANP(Analytic Network Process)と呼ばれている. 特に1990年前後からそのようなモデルの研究や応用が進んでいる[Saaty(1996), 高橋(1998)].  
82行目: 116行目:
  
 
[5] 高橋磐郎, 「講座:ＡＨＰからＡＮＰへの諸問題, I-V」, 『オペレーションズ・リサーチ』, 1998年1-5月号.
 
[5] 高橋磐郎, 「講座:ＡＨＰからＡＮＰへの諸問題, I-V」, 『オペレーションズ・リサーチ』, 1998年1-5月号.
 +
 +
[[category:AHP(階層的意思決定法)|えいえいちぴー]]

2007年8月7日 (火) 17:05時点における最新版

【えーえいちぴー (AHP (Analytic Hierarchy Process)) 】

　階層化意思決定法とも訳されるが, 通常AHPと呼ばれる. トマス・サーティー(Thomas L. Saaty)が, アメリカの政府機関でダンツィックらと数理計画の開発や応用をしていた経験から, トップの意思決定者が抱える構造がはっきりしなかったり複雑な問題を扱えるモデルや方法はないかと考えた上で, 開発された方法. 問題の構造を把握し難いときでも, 問題全体を, 究極の狙い, 評価基準, 代替案という階層図に表現することで明らかにした上で, 複数の評価基準のもとで, 多数の代替案の中からの選択, 複数の要素へのリソースの配分, あるいは複数の要素の評価や順位づけをする方法. 最終的には問題全体から見た代替案の重要度を求めるが, その基礎は, 2つの要素の一対比較という直感的で単純な判断の積み重ねで, これを基に問題全体の大局的な判断を支援する. 実際に組織の中だけではなく社会や公共の意思決定の場で広く実際に利用されている. [Saaty(1980, 1994), 刀根・真鍋(1990)]

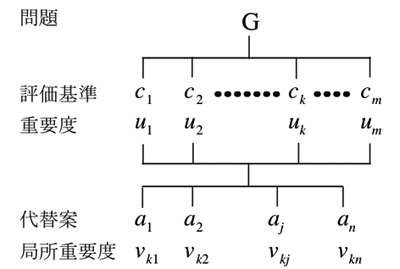
　[方法の概要]: AHPを用いて問題の解決を図るには, まず問題全体の構造を階層図(図1)に表す. もっとも簡単な構造は, 問題－評価基準－代替案の3層の図である. 評価基準の層の要素は互いに従属しないように選ぶ必要がある. その下に代替案を並べた層を設ける.


図１：階層図

図１：階層図


　この階層図の上で, 最上層の問題から見た各代替案の重要度を求めて意思決定の支援をしたいのである. そのためにはまず第1層の問題から見た第2層の評価基準 の重要度 を求める. さらに各評価基準 の下の代替案 の(局所)重要度 を求める. そのうえで, 代替案 ごとに, 各評価基準 の下での重要度 の, 評価基準の重要度 で重み付けをした和 を取って, 代替案 の(総合)重要度とする. この重要度を求める過程で一対比較評価をしている.

　[一対比較から重要度の計算へ]: 例えば評価基準が4つあったらそれらを , , , と表し, それぞれを要素と呼ぶ. 4要素あると 組の対があるのでそれらの対の2要素の重要さを比較判断する(一対比較する). 要素 を要素 と比べて値 を表1に従って定め, 行列に表したもの を一対比較行列と呼ぶ.


表１：一対比較の基準尺度
要素 が要素 に比べて
同程度に重要なとき 1
やや重要 3
かなり重要 5
非常に重要 7
圧倒的に重要 9
2, 4, 6, 8 という中間値も適宜使う.
とする.


　要素 の重要度(ウエイト (weight)あるいはプライオリティ (priority)とも呼ぶ)を とすると, を で推定していると考えられる. 行列 の要素 を で置き換えた上でベクトル を右から掛けると,




で, これは固有方程式 の形をしている. 行列 の階数は であり, の固有値は最大固有値が (要素数), その他のものは であることがいえるので, の最大固有値 に対する固有ベクトルを の値とする. この際に のすべての成分の和が であるほうが便利なので, の成分を正規化した(各成分をで割った)ものを重要度とする.

　[整合性]: 人間は一対比較で次のように整合性に欠ける判断をすることがある. (a)要素 AとBを比べるとBが好ましく, BとCを比べるとCが好ましいのに, AとCを比べるとAが好ましいとする. (b)AはBに比べて4倍程度強い, Cに比べると5倍くらい強いと判断したのに, BはCの7倍強いとする. もし整合性が完全にあれば, 3つの要素 の間で が成り立つはずである. 実際に整合性が完全にあると一対比較行列の最大固有値が要素の数に一致する()のでそのずれをの大きさによらぬようにした を整合度とする.この値がを超えると整合性が欠けることが強いので, 判断を再検討するなりやり直す必要があるとされている.

　また, 一対比較の結果に使われる数値をランダムに配置した同じサイズの多数の行列の整合度の平均値(ランダム整合度)に対するこの整合度の比(整合比)も以下が好ましいとされ, 整合性の判断に用いられている.

　[ANPへ]: AHPでは階層図の各層の要素の間には従属性がないものとしている. しかし実際には, 層の中の要素の間どころか, 上下の層の要素の間にも従属性が強い場合もある. そこまで拡張すると問題のモデルは階層図ではなくネットワークになってくるので, その分野はANP(Analytic Network Process)と呼ばれている. 特に1990年前後からそのようなモデルの研究や応用が進んでいる[Saaty(1996), 高橋(1998)].

　[AHPのソフトウエア]: 実際の意思決定にAHPを使うには, そのためのソフトウエアを使うと便利である. 階層図を書くこと, 一対比較をすることの支援, 代替案の総合重要度の計算から, 評価基準の重要度の代替案の重要度に対する感度分析をすることまで助けてくれる.

　海外ではWindows用の "Expert Choice"がMS-DOS時代から数えると10回以上の改良の版を重ねて国際的にも広く使われている(アメリカExpert Choice社, 国内代理店:ディエムエス(株)が日本語版も出している). フィンランドのRaimo Hamalainenはヨーロッパの複数の国語を扱えるソフトを出している. 日本では(株)日本科学技術研修所の「ねまわしくん」がかなり普及している.


参考文献

[1] T. L. Saaty, The Analytic Hierarchy Process, McGraw Hill, 1980. Reprinted as Vol. 1 of the AHP Series by RWS Publications, 1992.

[2] T. L. Saaty, Fundamentals of Decision Making and Priority Theory with the Analytic Hierarchy Process, Vol. VI of the AHP Series, PWS Publications, 1994.

[3] T. L. Saaty, Decision Making with Dependence and Feedback: Analytic Network Process, RWS Publications, 1996.

[4] 刀根 薫, 真鍋龍太郎編, 『ＡＨＰ事例集』, 日科技連出版社, 1990.

[5] 高橋磐郎, 「講座:ＡＨＰからＡＮＰへの諸問題, I-V」, 『オペレーションズ・リサーチ』, 1998年1-5月号.

「https://orsj-ml.org/orwiki/wiki/index.php?title=《AHP》&oldid=8033」から取得