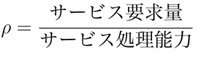「利用率」の版間の差分
ナビゲーションに移動
検索に移動
(新しいページ: ''''【りようりつ (traffic intensity)】''' 待ち行列モデルにおいて, 負荷の程度を表す重要なパラメータで, \[ \rho = \frac{\mbox{サービス要...') |
Albeit-Kun (トーク | 投稿記録) |
||
| (4人の利用者による、間の8版が非表示) | |||
| 1行目: | 1行目: | ||
'''【りようりつ (traffic intensity)】''' | '''【りようりつ (traffic intensity)】''' | ||
| − | 待ち行列モデルにおいて, 負荷の程度を表す重要なパラメータで, \[ | + | 待ち行列モデルにおいて, 負荷の程度を表す重要なパラメータで, |
| + | |||
| + | <center><table><tr><td align=center>[[画像:sy-b-a-01-92f.png]]</td></tr> | ||
| + | <td align=center> | ||
| + | </td></table></center> | ||
| + | |||
| + | <!-- | ||
| + | \[ | ||
| + | \rho = \frac{\mbox{サービス要求量}}{\mbox{サービス処理能力}} | ||
| + | \] | ||
| + | --> | ||
| + | |||
| + | で定義される. 待合室の容量が無限のモデルでは, システムが平衡状態に向かうための条件が <math>\rho<1\,</math> である. 標準的な GI/G/<math>c\,</math> モデルでは, 平均到着間隔を <math>\lambda^{-1}\,</math>, 平均サービス時間を <math>\mu^{-1}\,</math> としたとき, <math>\rho=\lambda/(c \mu)\,</math> で与えられる. | ||
| + | |||
| + | [[category:待ち行列|りようりつ]] | ||