「運搬経路問題」の版間の差分
細 ("運搬経路問題" を保護しました。 [edit=sysop:move=sysop]) |
Albeit-Kun (トーク | 投稿記録) |
||
| (2人の利用者による、間の2版が非表示) | |||
| 1行目: | 1行目: | ||
'''【うんぱんけいろもんだい (vehicle routing problem (VRP))】''' | '''【うんぱんけいろもんだい (vehicle routing problem (VRP))】''' | ||
| + | === 概要 === | ||
| + | デポ(depot)と呼ばれる特定の施設に待機する運搬車によって, 顧客の需要を運搬(または収集)し, 再びデポに戻る. このとき顧客の位置・需要量・作業時間, 利用可能な運搬車台数ならびに運搬車の最大積載量・最大稼働時間, 地点間の移動時間・移動距離・移動費用などが与えられたとき, 総移動時間・総移動距離・総移動費用・必要な運搬車台数などを最小化する顧客訪問順(ルート)を求める問題. | ||
| + | |||
| + | === 詳説 === | ||
| + | |||
| + | [[運搬経路問題]] (vehicle routing problem) [[配送計画問題]], [[トラック配送問題]], [[配送問題]], [[輸送経路問題]])とは, デポ(depot)とよばれる特定の施設に待機する運搬車によって, 顧客の需要を運搬(または収集)する最小コストのルートを求める問題の総称である [3]. | ||
| + | |||
| + | |||
| + | <center><table><tr><td align=center>[[画像:0173-C-C-02+zu1.png|center|図1:運搬経路問題の概念図]]</td></tr> | ||
| + | <td align=center><br>図1:運搬経路問題の概念図</td></table></center> | ||
| + | |||
| + | |||
| + | |||
| + | 運搬経路問題の適用分野には, 店舗への配送, 郵便や新聞の配達, ゴミの収集, 航空機の路線決定や乗務員のスケジューリング等の広範囲な領域が対象として含まれる. | ||
| + | |||
| + | 以下に代表的な構成要素に基づく分類を示す. | ||
| + | |||
| + | |||
| + | :1. デポ数に基づく分類 | ||
| + | |||
| + | ::デポ数が単一か複数かに分類される. | ||
| + | |||
| + | :2. 運搬車の種類に基づく分類 | ||
| + | |||
| + | ::運搬車の区別をしない場合(等質:homogeneous)と区別をする場合(非等質:heterogeneous)に分類される. | ||
| + | |||
| + | :3. 顧客上での作業内容に基づく分類 | ||
| + | |||
| + | ::積み込みまたは積み下ろしのみか, 積み込み・積み下ろしの混合に分類される. | ||
| + | |||
| + | :4. 顧客への到着時刻に基づく分類 | ||
| + | |||
| + | ::(a) 到着時刻に指定なし | ||
| + | |||
| + | :::通常の運搬経路問題に対する仮定である. | ||
| + | |||
| + | ::(b) 到着時刻が指定 | ||
| + | |||
| + | :::[[運搬車スケジューリング問題]] (vehicle scheduling problem)とよばれる. バスの運行スケジュールや飛行機の[[乗務員スケジューリング問題]] (crew scheduling problem)への応用をもつ. | ||
| + | |||
| + | ::(c) 到着時刻が何時から何時までと時間枠(time window)で指定 | ||
| + | |||
| + | :::[[時間枠付き運搬経路問題]] (vehicle routing problem with time windows)とよばれる. | ||
| + | |||
| + | :5. 需要が発生する場所に基づく分類 | ||
| + | |||
| + | ::(a) 顧客(点)上 | ||
| + | |||
| + | :::通常の運搬経路問題に対する仮定である. | ||
| + | |||
| + | ::(b) 枝(ネットワーク上の2点間)上 | ||
| + | |||
| + | :::枝巡回路問題(arc routing problem)とよばれ, 郵便配達人, 除雪車や道路清掃車の巡回経路を求める問題への応用をもつ. 枝巡回路問題は対象とするネットワークに応じて, [[郵便配達人問題]] (postman problem)または[[中国郵便配達人問題]] (Chinese postman problem), 田舎の郵便配達人問題(rural postman problem)等に分類される. | ||
| + | |||
| + | また上記の他に, 顧客を訪問するパターンの中から1つを選択し, 一定期間におけるルートの最適化を目的とした多期間運搬経路問題(multi-period vehicle routing problem), 顧客を訪問する頻度を運搬に関わる費用と顧客上での在庫費用とのトレードオフによって制御する[[在庫運搬経路問題]] (inventory vehicle routing problem)等のバリエーションがある. | ||
| + | |||
| + | 運搬経路問題のバリエーションのほとんどはNP困難(NP-hard)であり, 多項式時間の厳密解法は絶望視されている[4] . 近似解法としては, 古典的なものとして[[セービング法]] (saving method)([[クラーク・ライト法]], [[節約法]])が挙げられる. 多くの近似解法は, 顧客をグループ(クラスター)に分割した後に, 個々のクラスターに対してルートを設定する解法, クラスター先・ルート後法(cluster-first/route-second method)に基づいている. クラスターへの分割に関しては, 1970年代には [[領域分割法]] (region partitioning method)が中心に用いられており, 1980年代以降には[[一般化割当法 (運搬経路問題における)|一般化割当法]] (generalized assignment method), 漸近的最適性をもつ[[施設配置ヒューリスティック (運搬経路問題の)|施設配置ヒューリスティック]] (location based heuristic) [2] の有効性が認識されている. また1990年代には, 得られる解の精度だけでなく現実問題に対する頑健性よりメタ解法(meta-heuristics)が注目され, 解法の実装に関しては, GIS (geographic information system)を中心とした情報技術との連携による構築・導入事例が評価されている [1]. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ---- | ||
| + | '''参考文献''' | ||
| + | |||
| + | [1] J. Braca, J. Bramel, B. Posner and D. Simchi-Levi, "A Computerized Approach to the New York City School Bus Routing Problem," ''IIE Transactions'', '''29''' (1997), 693-702. | ||
| + | |||
| + | [2] J. Bramel and D. Simchi-Levi, "A Location Based Heuristic for General Routing Problems," ''Operations Research'', '''43''' (1995), 649-660. | ||
| − | + | [3] G. Laporte and I. H. Osman, "Routing Problems: A Bibliography, " ''Annals of Operations Research'', '''61''' (1995), 227-262. | |
| + | |||
| + | [4] J. K. Lenstra and A. H. G. Rinnooy-Kan, "Complexity of Vehicle Routing and Scheduling Problems," ''Networks'', '''11''' (1981), 221-227. | ||
| + | |||
| + | [[category:生産・在庫・ロジスティクス|うんぱんけいろもんだい]] | ||
| + | |||
| + | [[category:企画・開発・プロジェクト・品質・ヒューマン|うんぱんけいろもんだい]] | ||
2008年11月7日 (金) 14:34時点における最新版
【うんぱんけいろもんだい (vehicle routing problem (VRP))】
概要
デポ(depot)と呼ばれる特定の施設に待機する運搬車によって, 顧客の需要を運搬(または収集)し, 再びデポに戻る. このとき顧客の位置・需要量・作業時間, 利用可能な運搬車台数ならびに運搬車の最大積載量・最大稼働時間, 地点間の移動時間・移動距離・移動費用などが与えられたとき, 総移動時間・総移動距離・総移動費用・必要な運搬車台数などを最小化する顧客訪問順(ルート)を求める問題.
詳説
運搬経路問題 (vehicle routing problem) 配送計画問題, トラック配送問題, 配送問題, 輸送経路問題)とは, デポ(depot)とよばれる特定の施設に待機する運搬車によって, 顧客の需要を運搬(または収集)する最小コストのルートを求める問題の総称である [3].
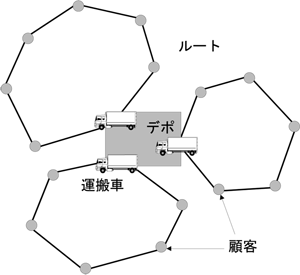
図1:運搬経路問題の概念図 |
運搬経路問題の適用分野には, 店舗への配送, 郵便や新聞の配達, ゴミの収集, 航空機の路線決定や乗務員のスケジューリング等の広範囲な領域が対象として含まれる.
以下に代表的な構成要素に基づく分類を示す.
- 1. デポ数に基づく分類
- デポ数が単一か複数かに分類される.
- 2. 運搬車の種類に基づく分類
- 運搬車の区別をしない場合(等質:homogeneous)と区別をする場合(非等質:heterogeneous)に分類される.
- 3. 顧客上での作業内容に基づく分類
- 積み込みまたは積み下ろしのみか, 積み込み・積み下ろしの混合に分類される.
- 4. 顧客への到着時刻に基づく分類
- (a) 到着時刻に指定なし
- 通常の運搬経路問題に対する仮定である.
- (b) 到着時刻が指定
- 運搬車スケジューリング問題 (vehicle scheduling problem)とよばれる. バスの運行スケジュールや飛行機の乗務員スケジューリング問題 (crew scheduling problem)への応用をもつ.
- (c) 到着時刻が何時から何時までと時間枠(time window)で指定
- 時間枠付き運搬経路問題 (vehicle routing problem with time windows)とよばれる.
- 5. 需要が発生する場所に基づく分類
- (a) 顧客(点)上
- 通常の運搬経路問題に対する仮定である.
- (b) 枝(ネットワーク上の2点間)上
また上記の他に, 顧客を訪問するパターンの中から1つを選択し, 一定期間におけるルートの最適化を目的とした多期間運搬経路問題(multi-period vehicle routing problem), 顧客を訪問する頻度を運搬に関わる費用と顧客上での在庫費用とのトレードオフによって制御する在庫運搬経路問題 (inventory vehicle routing problem)等のバリエーションがある.
運搬経路問題のバリエーションのほとんどはNP困難(NP-hard)であり, 多項式時間の厳密解法は絶望視されている[4] . 近似解法としては, 古典的なものとしてセービング法 (saving method)(クラーク・ライト法, 節約法)が挙げられる. 多くの近似解法は, 顧客をグループ(クラスター)に分割した後に, 個々のクラスターに対してルートを設定する解法, クラスター先・ルート後法(cluster-first/route-second method)に基づいている. クラスターへの分割に関しては, 1970年代には 領域分割法 (region partitioning method)が中心に用いられており, 1980年代以降には一般化割当法 (generalized assignment method), 漸近的最適性をもつ施設配置ヒューリスティック (location based heuristic) [2] の有効性が認識されている. また1990年代には, 得られる解の精度だけでなく現実問題に対する頑健性よりメタ解法(meta-heuristics)が注目され, 解法の実装に関しては, GIS (geographic information system)を中心とした情報技術との連携による構築・導入事例が評価されている [1].
参考文献
[1] J. Braca, J. Bramel, B. Posner and D. Simchi-Levi, "A Computerized Approach to the New York City School Bus Routing Problem," IIE Transactions, 29 (1997), 693-702.
[2] J. Bramel and D. Simchi-Levi, "A Location Based Heuristic for General Routing Problems," Operations Research, 43 (1995), 649-660.
[3] G. Laporte and I. H. Osman, "Routing Problems: A Bibliography, " Annals of Operations Research, 61 (1995), 227-262.
[4] J. K. Lenstra and A. H. G. Rinnooy-Kan, "Complexity of Vehicle Routing and Scheduling Problems," Networks, 11 (1981), 221-227.